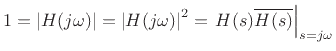Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
As discussed in §B.2, the an allpass filter can be defined
as any filter that preserves signal energy for every input
signal 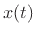 . In the continuous-time case, this means
. In the continuous-time case, this means
where 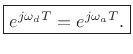 denotes the output signal, and
denotes the output signal, and
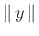 denotes the
denotes the
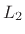 norm of
norm of 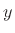 . Using the Rayleigh energy theorem
(Parseval's theorem) for Fourier transforms [87],
energy preservation can be expressed in the frequency domain by
. Using the Rayleigh energy theorem
(Parseval's theorem) for Fourier transforms [87],
energy preservation can be expressed in the frequency domain by
where 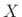 and
and 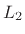 denote the Fourier transforms of
denote the Fourier transforms of  and
and 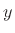 , respectively,
and frequency-domain
, respectively,
and frequency-domain 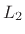 norms are defined by
norms are defined by
If 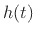 denotes the impulse response of the allpass
filter, then its transfer function
denotes the impulse response of the allpass
filter, then its transfer function 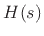 is given by the Laplace transform of
is given by the Laplace transform of 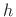 ,
,
and we have the requirement
Since this equality must hold for every input signal  , it must be
true in particular for complex sinusoidal inputs of the form
, it must be
true in particular for complex sinusoidal inputs of the form
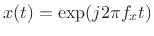 , in which case [87]
, in which case [87]
where 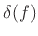 denotes the Dirac ``delta function'' or continuous
impulse function (§E.4.3). Thus, the allpass condition becomes
denotes the Dirac ``delta function'' or continuous
impulse function (§E.4.3). Thus, the allpass condition becomes
which implies
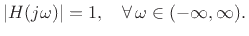 |
(E.13) |
Suppose 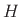 is a rational analog filter, so that
is a rational analog filter, so that
where 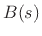 and
and 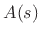 are polynomials in
are polynomials in  :
:
(We have normalized 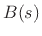 so that
so that 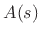 is monic (
is monic (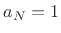 ) without
loss of generality.) Equation (E.13) implies
) without
loss of generality.) Equation (E.13) implies
If 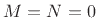 , then the allpass condition reduces to
, then the allpass condition reduces to
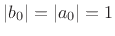 ,
which implies
,
which implies
where
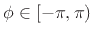 is any real phase constant. In other words,
is any real phase constant. In other words,
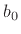 can be any unit-modulus complex number. If
can be any unit-modulus complex number. If 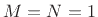 , then the
filter is allpass provided
, then the
filter is allpass provided
Since this must hold for all 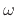 , there are only two solutions:
, there are only two solutions:
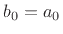 and
and 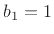 , in which case
, in which case
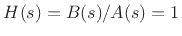 for all
for all  .
.
-
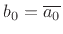 and
and 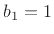 , i.e.,
, i.e.,
Case (1) is trivially allpass, while case (2) is the one discussed above
in the introduction to this section.
By analytic continuation, we have
If 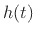 is real, then
is real, then
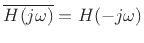 , and we can write
, and we can write
To have
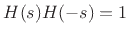 , every pole at
, every pole at 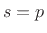 in
in 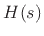 must be canceled
by a zero at
must be canceled
by a zero at 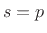 in
in 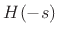 , which is a zero at
, which is a zero at 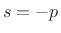 in
in  .
Thus, we have derived the simplified ``allpass rule'' for real analog
filters.
.
Thus, we have derived the simplified ``allpass rule'' for real analog
filters.
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]
![]() . In the continuous-time case, this means
. In the continuous-time case, this means
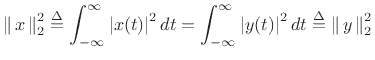
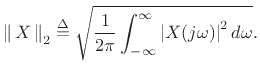
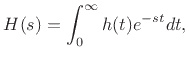
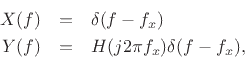
![]() denotes the Dirac ``delta function'' or continuous
impulse function (§E.4.3). Thus, the allpass condition becomes
denotes the Dirac ``delta function'' or continuous
impulse function (§E.4.3). Thus, the allpass condition becomes
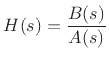
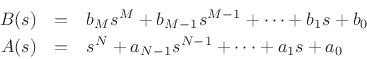
![]() so that
so that ![]() is monic (
is monic (![]() ) without
loss of generality.) Equation (E.13) implies
) without
loss of generality.) Equation (E.13) implies