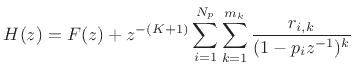Parallel First and/or Second-Order Sections

Instead of breaking up a filter into a series of second-order sections, as discussed in the previous section, we can break the filter up into a parallel sum of first and/or second-order sections. Parallel sections are based directly on the partial fraction expansion (PFE) of the filter transfer function discussed in §6.8. As discussed in §6.8.3, there is additionally an FIR part when the order of the transfer-function denominator does not exceed that of the numerator (i.e., when the transfer function is not strictly proper). The most general case of a PFE, valid for any finite-order transfer function, was given by Eq.$\,$(6.19), repeated here for convenience:

$$H(z) = F(z) + z^{-(K+1)}\sum_{i=1}^{N_p}\sum_{k=1}^{m_k}\frac{r_{i,k}}{(1-p_iz^{-1})^k} \protect$$ (10.2)

where $N_p$ denotes the number of distinct poles, and $m_i\ge 1$ denotes the multiplicity of the $i$th pole. The polynomial $F(z)$ is the transfer function of the FIR part, as discussed in §6.8.3.

The FIR part $F(z)$ is typically realized as a tapped delay line, as shown in Fig.5.5.