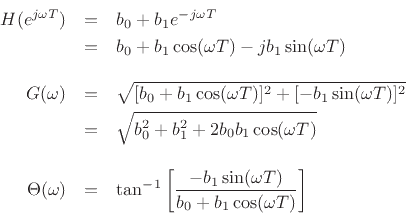 |
Fig.B.3 gives the signal flow graph for the general one-pole filter. The road to the frequency response goes as follows:
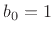 |
![\fbox{
\begin{tabular}{rl}
Difference equation: & $y(n) = b_0 x(n) - a_1 y(n-1)$\\ [5pt]
{\it z} transform: & $Y(z) = b_0 X(z) - a_1 z^{-1}Y(z)$\\ [5pt]
Transfer function: & $H(z) = \displaystyle\frac{b_0}{1+a_1z^{-1}}$\\ [5pt]
Frequency response: & $H(e^{j\omega T}) = \displaystyle\frac{b_0}{1+a_1e^{-j\omega T}}$
\end{tabular}}](img1359.png)
The one-pole filter has a transfer function (hence frequency response) which is the reciprocal of that of a one-zero. The analysis is thus quite analogous. The frequency response in polar form is given by
![\begin{eqnarray*}
G(\omega) &=& \frac{\vert b_0\vert}{\sqrt{[1 + a_1 \cos(\omega T)]^2 + [-a_1 \sin(\omega T)]^2}}\\
&=& \frac{\vert b_0\vert}{\sqrt{1 + a_1^2 + 2a_1 \cos(\omega T)}}\\ [10pt]
\Theta(\omega) &=&
\left\{\begin{array}{ll}
-\tan^{-1}\left[\frac{-a_1 \sin(\omega T)}{1 + a_1 \cos(\omega T)}\right], & b_0>0 \\ [5pt]
\pi-\tan^{-1}\left[\frac{-a_1 \sin(\omega T)}{1 + a_1 \cos(\omega T)}\right], & b_0<0 \\
\end{array} \right..
\end{eqnarray*}](img1360.png)
A plot of the frequency response in polar form for ![]() and
various values of
and
various values of ![]() is given in Fig.B.4.
is given in Fig.B.4.
The filter has a pole at ![]() , in the
, in the ![]() plane (and a zero at
plane (and a zero at ![]() = 0). Notice that the one-pole exhibits
either a lowpass or a highpass frequency response, like the
one-zero. The lowpass character occurs when the pole is near the point
= 0). Notice that the one-pole exhibits
either a lowpass or a highpass frequency response, like the
one-zero. The lowpass character occurs when the pole is near the point
![]() (dc), which happens when
(dc), which happens when ![]() approaches
approaches ![]() . Conversely,
the highpass nature occurs when
. Conversely,
the highpass nature occurs when ![]() is positive.
is positive.
The one-pole filter section can achieve much more drastic differences
between the gain at high frequencies and the gain at low frequencies
than can the one-zero filter. This difference is achieved in the
one-pole by gain boost in the passband rather than
attenuation in the stopband; thus it is usually desirable when
using a one-pole filter to set ![]() to a small value, such as
to a small value, such as
![]() , so that the peak gain is 1 or so. When the peak gain is 1,
the filter is unlikely to overflow.B.1
, so that the peak gain is 1 or so. When the peak gain is 1,
the filter is unlikely to overflow.B.1
Finally, note that the one-pole filter is stable if and only if
![]() .
.