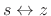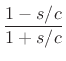Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Bilinear Transformation
The bilinear transformation may be defined by
where  is an arbitrary positive constant that we may set to map one
analog frequency precisely to one digital frequency. In the case of a
lowpass or highpass filter,
is an arbitrary positive constant that we may set to map one
analog frequency precisely to one digital frequency. In the case of a
lowpass or highpass filter,  is typically used to set the
cut-off frequency to be identical in the analog and digital
cases. The bilinear tranform was introduced in 1947I.2 for discrete-time filter analysis (a
year after the first general-purpose computer--the ENIAC--was
announced) by Arnold Tustin,I.3 so it is also called
``Tustin's Method.''
is typically used to set the
cut-off frequency to be identical in the analog and digital
cases. The bilinear tranform was introduced in 1947I.2 for discrete-time filter analysis (a
year after the first general-purpose computer--the ENIAC--was
announced) by Arnold Tustin,I.3 so it is also called
``Tustin's Method.''
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
[How to cite this work] [Order a printed hardcopy] [Comment on this page via email]