This chapter introduces the Discrete Fourier Transform (DFT) and
points out the mathematical elements that will be explicated in this
book. To find motivation for a detailed study of the DFT, the reader
might first peruse Chapter 8 to get a feeling for some of the many
practical applications of the DFT. (See also the preface on page
![]() .)
.)
Before we get started on the DFT, let's look for a moment at the
Fourier transform (FT) and explain why we are not talking about
it instead. The Fourier transform of a continuous-time signal ![]() may be defined as
may be defined as
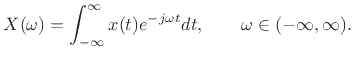
Thus, right off the bat, we need calculus. The DFT, on the other hand, replaces the infinite integral with a finite sum:
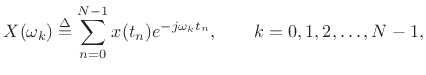
where the various quantities in this formula are defined on the next page. Calculus is not needed to define the DFT (or its inverse, as we will see), and with finite summation limits, we cannot encounter difficulties with infinities (provided