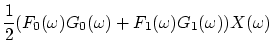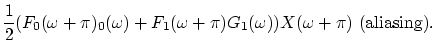Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Subband Coders
Subband splitting of a signal is often performed with a two-channel uniform
filterbank. The filterbank is used several times to achieve finer
bandsplitting, in a filter tree:
This way, the coder can split the input data into uniform bands,
in each of which a quantizer, adopted to the
masking threshold (see section 3), is applied.
The filterbank filterbank consists of four filters, 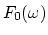 ,
,
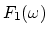 ,
, 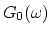 and
and 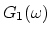 . The
. The  's are used to
split the input data in a high and a low frequency band. Both bands are
then subsampled with a factor of 2. To reconstruct, both bands are
upsampled again, and filtered with the
's are used to
split the input data in a high and a low frequency band. Both bands are
then subsampled with a factor of 2. To reconstruct, both bands are
upsampled again, and filtered with the 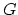 's. Thus, the output
's. Thus, the output
 can be written as
can be written as
To obtain aliasing cancellation, the following is required:
Optimally,
![\begin{displaymath}
\frac{1}{2}(F_0(\omega)G_0(\omega)+F_1(\omega)G_1(\omega)) = 1,
\ \omega\in[0..\pi],
\end{displaymath}](img19.png) |
(4) |
so that perfect reconstruction is achieved. This is, though, often hard to
achieve. The filters used in most coders are Quadrature Mirror Filters
(QMF), which achieve aliasing cancellation by choosing 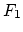 as the mirror
image of
as the mirror
image of  (around
(around 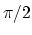 ):
):
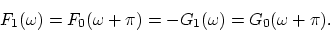 |
(5) |
To get good reconstruction without relying on the aliasing cancellation,
which cannot be relied on in the presence of quantization noise,
the QMF filters
have to have a steep pass-to-stop-band transition.
Subsections
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download bosse.pdf
![]() ,
,
![]() ,
, ![]() and
and ![]() . The
. The ![]() 's are used to
split the input data in a high and a low frequency band. Both bands are
then subsampled with a factor of 2. To reconstruct, both bands are
upsampled again, and filtered with the
's are used to
split the input data in a high and a low frequency band. Both bands are
then subsampled with a factor of 2. To reconstruct, both bands are
upsampled again, and filtered with the ![]() 's. Thus, the output
's. Thus, the output
![]() can be written as
can be written as