Implemented Model for Spreading Function

A spreading function which takes into account both in-band masking and inter-band masking is (taken from [2])

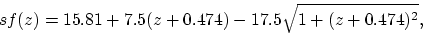$$sf(z) = 15.81+7.5(z+0.474)-17.5\sqrt{1+(z+0.474)^2},$$ (9)

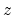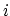where $z$ is the frequency in barks. This equation is modified to take into account the decreasing slope at higher masker amplitudes $i$ in the following manner:

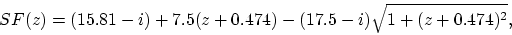$$SF(z) = (15.81-i)+7.5(z+0.474)-(17.5-i)\sqrt{1+(z+0.474)^2},$$ (10)

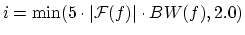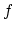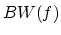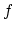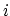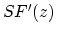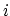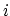where $i=\min(5\cdot \vert\mathcal{F}(f)\vert\cdot BW(f),2.0)$ , $f$ is the frequency of the masker and $BW(f)$ is the critical bandwidth at $f$. A higher value of $i$ gives a flatter $SF'(z)$, and the formula for $i$ is an experimentally found heuristic which compensates a frequency bin if it is only a small part of a wide critical band. Setting the max of $i$ to 2.0 was necessary for some test sounds, where e.g a base drum could make a large part of the high frequency spectra vanish. See Fig. 3 for an illustration of the spread function.

Figure 3: The masking spread function for a single masker. The scaled amplitude i varies from 0 to 2, where 2 corresponds to the wider spread.