Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Since we are working with sampled data, the ideal single-side-band
filter impulse response is
where 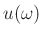 is a unit step function in the frequency domain:
is a unit step function in the frequency domain:
We can evaluate the IDTFT directly as follows:
For 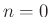 , going back to the original integral gives
, going back to the original integral gives
Thus, the real part of 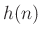 is
is
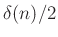 , and the imaginary part
is
, and the imaginary part
is 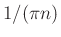 for odd
for odd 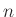 and zero otherwise (as a
result of bandlimiting). There is no aliasing.
and zero otherwise (as a
result of bandlimiting). There is no aliasing.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
[Comment on this page via email]
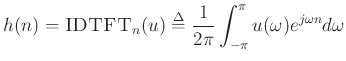
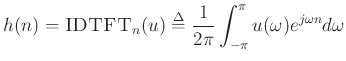
![$\displaystyle u(\omega) \isdef \left\{\begin{array}{ll}
1, & \omega\ge 0 \\ [5pt]
0, & \omega<0 \\
\end{array} \right.
$](img86.png)
![\begin{eqnarray*}
h(n) &=& \frac{1}{2\pi} \int_{0}^{\pi}e^{j\omega n} d\omega
= \left. \frac{1}{2\pi j n} e^{j\omega n} \right\vert _0^\pi
= \frac{e^{j\pi n}-1}{2\pi j n}\\ [10pt]
&=& \frac{(-1)^n-1}{2\pi j n}
= \left\{\begin{array}{ll}
0, & \hbox{$n$\ even}, n\neq 0 \\ [5pt]
j\dfrac{1}{\pi n}, & \hbox{$n$\ odd} \\
\end{array} \right.
\end{eqnarray*}](img87.png)
![]() , going back to the original integral gives
, going back to the original integral gives