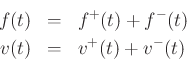
The actual ``travel time'' is always zero.
(For historical reasons, WDFs typically use traveling-wave components scaled by 2.)
- series (common velocity, summing forces), or
- parallel (common force, summing velocities).
Wave digital elements may be derived from their describing differential equations (in continuous time) as follows:
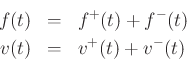
The actual ``travel time'' is always zero.
(For historical reasons, WDFs typically use traveling-wave components scaled by 2.)