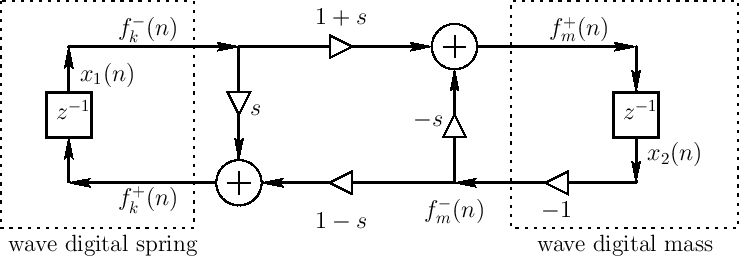
State variables labeled
Low-Frequency Analysis:
The reflection coefficient for our parallel force-wave connection is given as usual by the impedance step over the impedance sum:
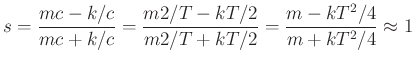
We can now see what's going physically at low frequencies relative to the sampling rate: