Classic WDF Wave Variables

We have been using our usual traveling-wave decomposition of force and velocity waves:

$$\begin{eqnarray*} f(t) &=& f^{{+}}(t)+f^{{-}}(t) \eqsp R_0v^{+}(t) - R_0v^{-}(t)\\ [5pt] v(t) &=& v^{+}(t)+v^{-}(t) \eqsp \frac{f^{{+}}(t)}{R_0} - \frac{f^{{-}}(t)}{R_0} \end{eqnarray*}$$

where $R_0$ is the wave impedance of the medium, or

$$\left[\begin{array}{c} f(t) \\ [2pt] v(t) \end{array}\right] = \left[\begin{array}{cc} R_0 & -R_0 \\ [2pt] 1 & 1 \end{array}\right] \left[\begin{array}{c} v^{+}(t) \\ [2pt] v^{-}(t) \end{array}\right] = \left[\begin{array}{cc} 1 & 1 \\ [2pt] \frac{1}{R_0} & -\frac{1}{R_0} \end{array}\right] \left[\begin{array}{c} f^{{+}}(t) \\ [2pt] f^{{-}}(t) \end{array}\right]$$

Inverting these gives

$$\begin{eqnarray*} \left[\begin{array}{c} v^{+}(t) \\ [2pt] v^{-}(t) \end{array}\right] &=& \frac{1}{2}\left[\begin{array}{cc} 1/R_0 & 1 \\ [2pt] -1/R_0 & 1 \end{array}\right]\left[\begin{array}{c} f(t) \\ [2pt] v(t) \end{array}\right]\\ [5pt] \left[\begin{array}{c} f^{{+}}(t) \\ [2pt] f^{{-}}(t) \end{array}\right] &=& \frac{1}{2}\left[\begin{array}{cc} 1 & R_0 \\ [2pt] 1 & -R_0 \end{array}\right]\left[\begin{array}{c} f(t) \\ [2pt] v(t) \end{array}\right] \end{eqnarray*}$$

In the WDF literature, the second case is typically used, multiplied by 2, and replacing force and velocity by voltage and current:

$$\begin{eqnarray*} a(t) &=& v(t)+R_0\,i(t)\\ b(t) &=& v(t)-R_0\,i(t) \end{eqnarray*}$$

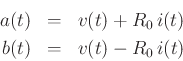
where $v(t)$ is now voltage and $i(t)$ denotes current. Thus, $a(t)=2v^+(t)$ and $b(t)=2v^-(t)$ (doubled voltage traveling-wave components)