Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Slope waves are simply related to velocity waves.
By the chain rule,
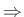
or
- Physical string slope = (lower rail - upper rail)/c
in a velocity-wave simulation
-
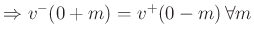 on a struck string
on a struck string
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download VariableChoice.pdf
Download VariableChoice_2up.pdf
Download VariableChoice_4up.pdf
![\begin{eqnarray*}
y'(t,x) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \frac{\partial}{\partial x}y(t,x) \\ [5pt]
&=& y'_r(t-x/c) + y'_l(t+x/c)
\\ [5pt]
&=& -\frac{1}{c} {\dot y}_r(t-x/c) + \frac{1}{c}{\dot y}_l(t+x/c) \\ [5pt]
&\rightarrow& -\frac{1}{c} v^{+}(n-m) + \frac{1}{c}v^{-}(n+m)
\end{eqnarray*}](img45.png)
![]()
![\begin{displaymath}
\begin{array}{rcrl}
y'^{+}&=&-&\frac{1}{c}v^{+}\\ [5pt]
y'^{-}&=&&\frac{1}{c}v^{-}
\end{array}\end{displaymath}](img47.png)
![\begin{displaymath}
\begin{array}{rcrl}
v^{+}&=&-&cy'^{+}\\ [5pt]
v^{-}&=&&cy'^{-}
\end{array}\end{displaymath}](img48.png)