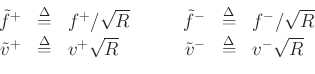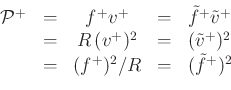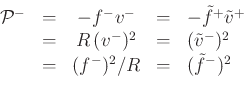Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Wave variables normalized to square root of power carried:
and
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download VariableChoice.pdf
Download VariableChoice_2up.pdf
Download VariableChoice_4up.pdf