Power Waves

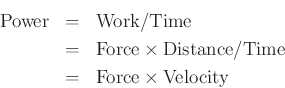
Physically,

$$\begin{eqnarray*} \hbox{Power} &=& \hbox{Work} / \hbox{Time} \\ &=& \hbox{Force} \times \hbox{Distance} / \hbox{Time} \\ &=& \hbox{Force} \times \hbox{Velocity} \end{eqnarray*}$$

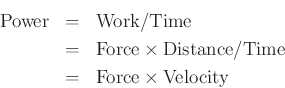
Traveling power waves:

$$\begin{array}{rcrl} {\cal P}^{+}(n) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}&&f^{{+}}(n)v^{+}(n) \\ {\cal P}^{-}(n) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}&-&f^{{-}}(n)v^{-}(n) \nonumber \end{array}$$

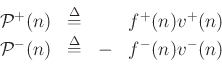
From ``Ohm's law'' $f^{{+}}= Rv^{+}$ and $f^{{-}}= -Rv^{-}$ , we have

$$\begin{eqnarray*} {\cal P}^{+}(n)&=&R\,[v^{+}(n)]^2=\frac{[f^{{+}}(n)]^2}{R} \\ {\cal P}^{-}(n)&=&R\,[v^{-}(n)]^2=\frac{[f^{{-}}(n)]^2}{R} \nonumber \end{eqnarray*}$$

Note that both ${\cal P}^{+}$ and ${\cal P}^{-}$ are nonnegative

Summing traveling powers gives total power:

$${\cal P}(t_n,x_m) \mathrel{\stackrel{\mathrm{\Delta}}{=}}{\cal P}^{+}(n-m) + {\cal P}^{-}(n+m)$$

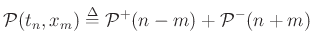
If we had instead defined 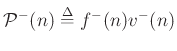${\cal P}^{-}(n) \mathrel{\stackrel{\mathrm{\Delta}}{=}}f^{{-}}(n)v^{-}(n)$ (no minus sign in front), then summing the traveling powers would give net power flow.