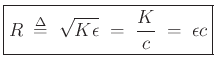Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
We just derived Ohm's Law for Traveling Waves on an Ideal String
where the velocity waves are defined in terms of transverse string displacement by
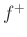 and
and 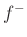 are corresponding force waves, and
are corresponding force waves, and
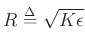 is the wave impedance of the string:
is the wave impedance of the string:
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download VariableChoice.pdf
Download VariableChoice_2up.pdf
Download VariableChoice_4up.pdf
![\fbox{%
\begin{minipage}[c]{3in}%
\begin{displaymath}\begin{array}{rcrl}%
f^{{+}}(n)&=&&R\,v^{+}(n) \\
f^{{-}}(n)&=&-&R\,v^{-}(n)
\end{array}\end{displaymath}\end{minipage}}](img55.png)
![\fbox{%
\begin{minipage}[c]{3in}%
\begin{displaymath}\begin{array}{rcrl}%
f^{{+}}(n)&=&&R\,v^{+}(n) \\
f^{{-}}(n)&=&-&R\,v^{-}(n)
\end{array}\end{displaymath}\end{minipage}}](img55.png)
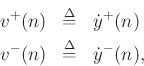
![]() and
and ![]() are corresponding force waves, and
are corresponding force waves, and
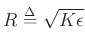 is the wave impedance of the string:
is the wave impedance of the string: