Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Energy density = potential + kinetic energy densities:
Sampled wave energy density can be expressed as
where
Total wave energy in string of length 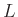 :
:
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download VariableChoice.pdf
Download VariableChoice_2up.pdf
Download VariableChoice_4up.pdf
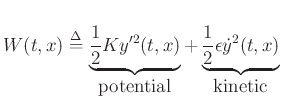
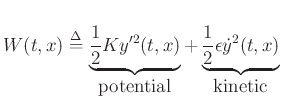
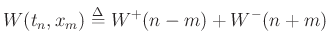
![\begin{eqnarray*}
W^{+}(n) &=& \frac{{\cal P}^{+}(n)}{c} = \frac{f^{{+}}(n)v^{+}(n)}{c}
= \epsilon \left[v^{+}(n)\right]^2 = \frac{\left[f^{{+}}(n)\right]^2}{K} \\
W^{-}(n) &=& \frac{{\cal P}^{-}(n)}{c} = -\frac{f^{{-}}(n)v^{-}(n)}{c}
= \epsilon \left[v^{-}(n)\right]^2 = \frac{\left[f^{{-}}(n)\right]^2}{K} \nonumber
\end{eqnarray*}](img88.png)
![]() :
:
