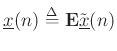
A similarity transformation of a state-space system is a linear change of state variable coordinates:
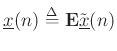
where
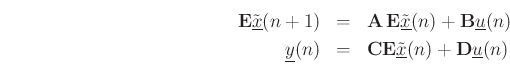
Premultiplying the first equation above by
![]() gives
gives
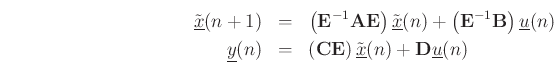
Define the transformed system matrices by

We can now write
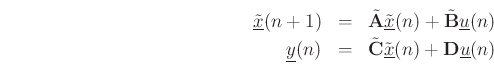
The transformed system describes the same system in new state-variable coordinates
Let's verify that the transfer function has not changed:
![\begin{eqnarray*}
{\tilde{\mathbf{H}}}(z) &=& \tilde{\mathbf{D}}+ \tilde{\mathbf{C}}(z\mathbf{I}- \tilde{\mathbf{A}})^{-1}\tilde{\mathbf{B}}\\
&=& \mathbf{D}+ (\mathbf{C}\mathbf{E}) \left(z\mathbf{I}- \mathbf{E}^{-1}\mathbf{A}\mathbf{E}\right)^{-1}(\mathbf{E}^{-1}\mathbf{B})\\
&=& \mathbf{D}+ \mathbf{C}\left[\mathbf{E}\left(z\mathbf{I}- \mathbf{E}^{-1}\mathbf{A}\mathbf{E}\right)\mathbf{E}^{-1}\right]^{-1} \mathbf{B}\\
&=& \mathbf{D}+ \mathbf{C}\left(z\mathbf{I}- \mathbf{A}\right)^{-1} \mathbf{B}= \mathbf{H}(z)
\end{eqnarray*}](img110.png)