Converting to State-Space Form by Hand

1. First, determine the filter transfer function $\mathbf{H}(z)$ . In the example, the transfer function can be written, by inspection, as
   $$\mathbf{H}(z) = \frac{1 + 2 z^{-1}+ 3 z^{-2}}{1 + \frac{1}{2}z^{-1}+ \frac{1}{3}z^{-2}}$$

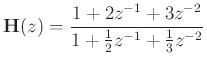
2. If ${\mathbf{h}}(0)\neq 0$ , we must ``pull out'' the parallel delay-free path:

   $$\mathbf{H}(z) = d_0 + \frac{b_1 z^{-1}+ b_2 z^{-2}}{1 + \frac{1}{2}z^{-1}+ \frac{1}{3}z^{-2}}$$
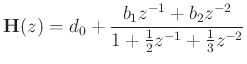
   Obtaining a common denominator and equating numerator coefficients yields
   $$\begin{eqnarray*} d_0 &=& 1\\ b_1 &=& 2 - \frac{1}{2}= \frac{3}{2}\\ [10pt] b_2 &=& 3 - \frac{1}{3}= \frac{8}{3} \end{eqnarray*}$$
   

   The same result is obtained using long or synthetic division

3. Next, draw the strictly causal part in direct form II, as shown below:

   
   

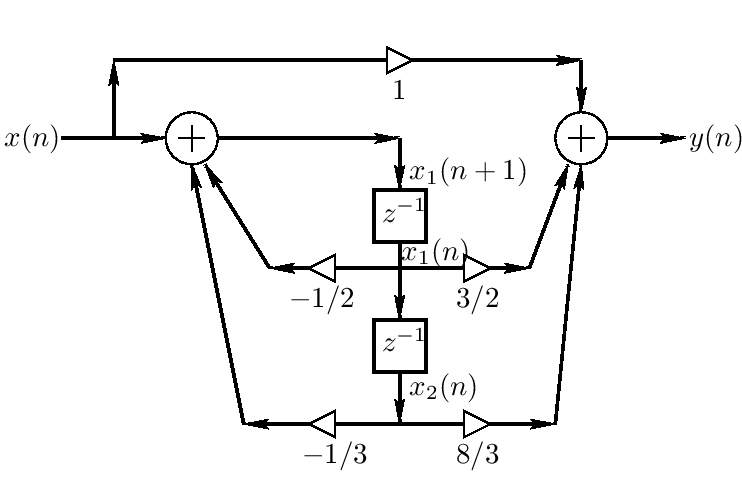
   It is important that the filter representation be canonical with respect to delay, i.e., the number of delay elements equals the order of the filter

4. Assign a state variable to the output of each delay element (see figure)

5. Write down the state-space representation by inspection. (Try it and compare to answer above.)