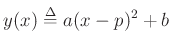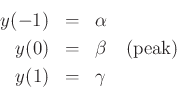Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
![\begin{psfrags}\psfrag{a} []{ \large$ \alpha $}\psfrag{b} []{ \large$ \beta $}\psfrag{g} []{ \large$ \gamma $\ }\begin{center}
\epsfig{file=eps/parabola.eps,width=6in} \\
\end{center} % was epsfbox
\end{psfrags}](img30.png)
Assume a parabola centered at 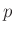 :
:
Evaluating at three adjacent bins about the peak, we have
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
[Comment on this page via email]
![\begin{psfrags}\psfrag{a} []{ \large$ \alpha $}\psfrag{b} []{ \large$ \beta $}\psfrag{g} []{ \large$ \gamma $\ }\begin{center}
\epsfig{file=eps/parabola.eps,width=6in} \\
\end{center} % was epsfbox
\end{psfrags}](img30.png)
![\begin{psfrags}\psfrag{a} []{ \large$ \alpha $}\psfrag{b} []{ \large$ \beta $}\psfrag{g} []{ \large$ \gamma $\ }\begin{center}
\epsfig{file=eps/parabola.eps,width=6in} \\
\end{center} % was epsfbox
\end{psfrags}](img30.png)
![]() :
: