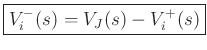Four Ideal Strings Intersecting at a Load
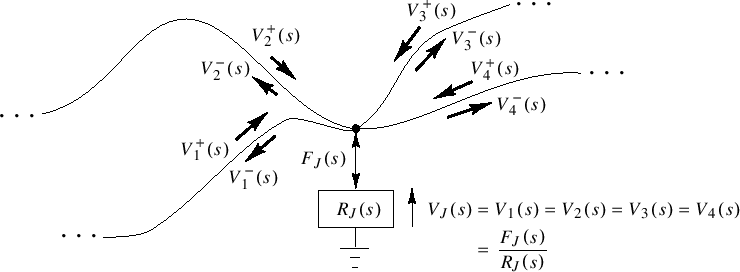
Series junction
![]() common velocity,
forces sum to 0:
common velocity,
forces sum to 0:
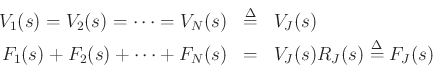
Computing common velocity at junction:
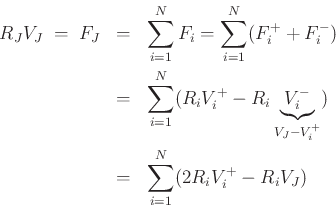
![]()
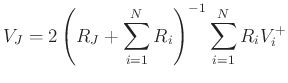
or
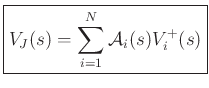
where
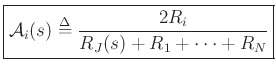
(generalized ``alpha parameter'', cf. Wave Digital Filters)
Finally, by continuity,
![]()