Scattering Solution

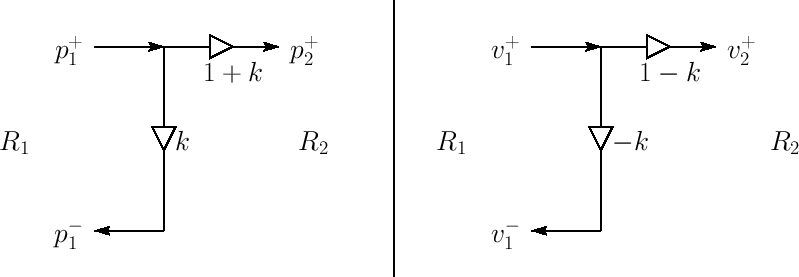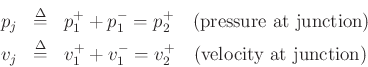
Let

$$\begin{eqnarray*} p_j &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& p^+_1+p^-_1 = p^+_2\quad\mbox{(pressure at junction)}\\ v_j &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& v^{+}_1+v^{-}_1 = v^{+}_2\quad\mbox{(velocity at junction)} \end{eqnarray*}$$

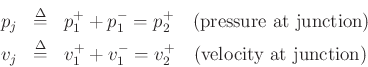
Then we can write

$$\begin{eqnarray*} p^+_1+p^-_1 &=& p^+_2\;=\;p_j\\ [10pt] \,\,\Rightarrow\,\,R_1v^{+}_1 - R_1v^{-}_1 &=& R_2 v^{+}_2 \;=\; R_2 v_j\\ [10pt] \,\,\Rightarrow\,\,R_1v^{+}_1 - R_1(v_j-v^{+}_1) &=& R_2 v_j\\ [10pt] \,\,\Rightarrow\,\,2\,R_1v^{+}_1 - R_1 v_j &=& R_2 v_j \end{eqnarray*}$$

$$\,\,\Rightarrow\,\,\zbox{v_j = \frac{2\,R_1}{R_1 + R_2}v^{+}_1}$$

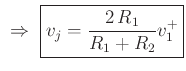
We have solved for the junction velocity $v_j=v^{+}_2$ . The transmitted pressure is then $p^+_2 = R_2v^{+}_2 = R_2 v_j$ .

Since $v_j = v^{+}_1+v^{-}_1$ , the reflected velocity is simply

$$v^{-}_1 = v_j - v^{+}_1 = \left[\frac{2\,R_1}{R_1+R_2} - 1\right]v^{+}_1 = \frac{R_1-R_2}{R_1+R_2} v^{+}_1$$

Thus, we have solved for the transmitted and reflected velocity waves given the incident wave and the two impedances.

Using the Ohm's law relations, the pressure waves follow:

$$\begin{eqnarray*} p^+_2 &=& R_2v^{+}_2 = R_2 v_j = \frac{2\,R_2}{R_1+R_2}p^+_1\\ [10pt] p^-_1 &=& -R_1v^{-}_1 = \frac{R_2-R_1}{R_1+R_2} p^+_1 \end{eqnarray*}$$

Define

$$\zbox{k= \frac{R_2-R_1}{R_1+R_2} = \frac{\mbox{Impedance Step}}{\mbox{Impedance Sum}}}$$

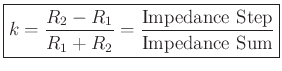
Then we get the following scattering relations in terms of $k$ for pressure waves:

Signal Flow Graph:

Signal power conserved (left-going power negated):

$$p^+_1v^{+}_1 = p^+_2v^{+}_2 + ( - p^-_1v^{-}_1)$$