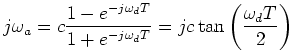The Bilinear Transform

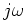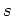A class of bilinear transforms map the entire $j\omega$ axis in the $s$ plane exactly once to the unit circle in the 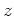$z$ plane:

$$s = c \frac{1-z^{-1}}{1+z^{-1}}$$

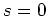• dc ($s=0$) maps to dc (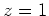$z=1$) as for the FDA
• infinite frequency (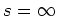$s=\infty$) maps to half the sampling rate (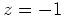$z=-1$) instead of 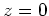$z=0$ for the FDA
• damping characteristics are better preserved
• no aliasing (mapping is one-to-one)
• frequency axis remains warped away from dc

The real constant 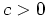$c>0$ allows one nonzero frequency (at 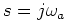$s=j\omega_a$) to map exactly to any desired digital frequency (at 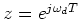$z=e^{j\omega_dT}$). All other frequencies are warped:

$$j\omega_a = c \frac{1-e^{-j\omega_d T}}{1+e^{-j\omega_d T}} = jc\tan\left(\frac{\omega_d T}{2}\right)$$