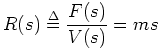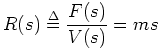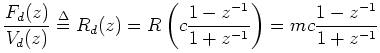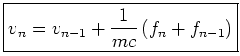Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Starting with the driving point impedance
the bilinear transform gives the digital impedance
Multiplying out
and taking the inverse 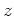 transform gives
or
(The
transform gives
or
(The 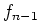 term is new relative to the FDA.)
term is new relative to the FDA.)
Can check: Equivalent to trapezoid rule for numerical integration
Subsections
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download SMAC03S.pdf
Download SMAC03S_2up.pdf