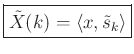The Discrete Fourier Transform

The ``$k$ th bin'' of the Discrete Fourier Transform (DFT) is defined as

$$\begin{eqnarray*} X(k) &\mathrel{\stackrel{\Delta}{=}}& \hbox{\sc DFT}_k(x) \mathrel{\stackrel{\Delta}{=}}\left<x,s_k\right> \mathrel{\stackrel{\Delta}{=}}\sum_{n=0}^{N-1}x(t_n)e^{-j\omega_kt_n} \\ [10pt] s_k(n) & \mathrel{\stackrel{\Delta}{=}}& e^{j\omega_k t_n}; \quad k=0,1,\ldots,N-1 \\ [15pt] \omega_k &\mathrel{\stackrel{\Delta}{=}}& 2\pi \frac{k}{N}f_s = \frac{2\pi k}{NT} ; \quad t_n \mathrel{\stackrel{\Delta}{=}}nT \end{eqnarray*}$$

The DFT is proportional the coefficients of projection of the signal vector $x$ onto the $N$ sinusoidal basis signals $s_k$ , $k=0,1,\ldots,N-1$ :

$$\zbox{X(k) = \left<x,s_k\right>}$$

The normalized DFT is precisely the coefficients of projection of the signal vector $x$ onto the $N$ normalized sinusoidal basis signals $\tilde{s}_k=s_k/\Vert s_k\Vert=s_k/\sqrt{N}$ :

$$\zbox{\tilde{X}(k) = \left<x,\tilde{s}_k\right>}$$