The downsampling operation
![]() selects every
selects every ![]() sample of
a signal:
sample of
a signal:

In the DFT case,
The Aliasing Theorem states that downsampling in time corresponds to aliasing in the frequency domain:
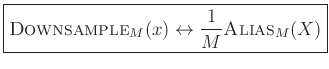
where the
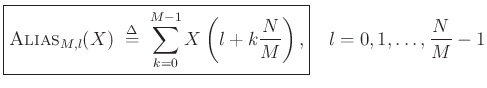
For
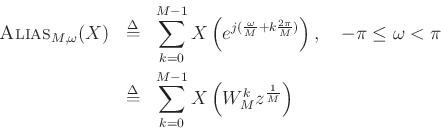
where
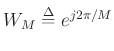 is a common notation for the primitive
is a common notation for the primitive
![]() th root of unity, and
th root of unity, and
![]() as usual. This normalization
corresponds to
as usual. This normalization
corresponds to ![]() after downsampling. Thus,
after downsampling. Thus, ![]() prior to
downsampling.
prior to
downsampling.
The summation terms above for ![]() are called aliasing
components.
are called aliasing
components.
The aliasing theorem points out that in order to downsample by factor
![]() without aliasing, we must first lowpass-filter the spectrum to
without aliasing, we must first lowpass-filter the spectrum to
![]() . This filtering essentially zeroes out
the spectral regions which alias upon sampling.
. This filtering essentially zeroes out
the spectral regions which alias upon sampling.