Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Now the system is in state space form, suppose we change to
diagonal coordinates:
where
The 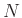 complex-conjugate-pair eigenvalues
complex-conjugate-pair eigenvalues
 represent the modal frequencies and dampings
represent the modal frequencies and dampings
- The main (desired) effect of the third order partial derivative
with respect to time is to make the damping factors
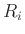 be smaller
for higher-frequency modes.
be smaller
for higher-frequency modes.
- A secondary effect is that the modal frequencies
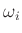 are
slightly shifted.
are
slightly shifted.
- Another secondary effect of the third-order time derivative is
the introduction of
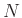 real rapidly decaying modes, characterized by
the
real rapidly decaying modes, characterized by
the
 . These eigenvalues are typically negligible.
. These eigenvalues are typically negligible.
We can reduce the size of the system to  , and further change
coordinates so that the matrix is made up of
, and further change
coordinates so that the matrix is made up of 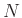 2 by 2 real ``modal''
blocks as follows:
2 by 2 real ``modal''
blocks as follows:
Next |
Prev |
Up |
Top
|
Index |
JOS Index |
JOS Pubs |
JOS Home |
Search
Download PianoString.pdf
Download PianoString_2up.pdf
Download PianoString_4up.pdf


![\begin{eqnarray*}
{\bf D} = {\left [\begin{matrix}
\left [\begin{matrix}
\lambda_{1} & & & & \cr
& \lambda_{1}^{*} & & & \cr
& & \ddots \cr & & \cr
& & & \lambda_{N} & \cr
& & & & \lambda_{N}^{*} \cr \end{matrix}\right ] & \cr
& \left [\begin{matrix}
\epsilon_{1} & & \cr
& \ddots & \cr
& & \epsilon_{N} \cr \end{matrix}\right]\end{matrix}\right ]}
\end{eqnarray*}](img44.png)
![]() complex-conjugate-pair eigenvalues
complex-conjugate-pair eigenvalues
![]() represent the modal frequencies and dampings
represent the modal frequencies and dampings
![]() , and further change
coordinates so that the matrix is made up of
, and further change
coordinates so that the matrix is made up of ![]() 2 by 2 real ``modal''
blocks as follows:
2 by 2 real ``modal''
blocks as follows:
![\begin{eqnarray*}
{\bf D^{''}} = {\left [\begin{matrix}
\left [\begin{matrix}
0 & 1 \cr -\vert\lambda_{1}\vert^{2} & 2Re(\lambda_{1})\end{matrix}\right ] & & & \cr
& \left [\begin{matrix}0 & 1 \cr -\vert\lambda_{2}\vert^{2} & 2Re(\lambda_{2})\end{matrix}\right ] & & \cr
& & \ddots & \cr
& & & \left [\begin{matrix}0 & 1 \cr -\vert\lambda_{N}\vert^{2} & 2Re(\lambda_{N})\end{matrix}\right ] \cr
\end{matrix}\right ]}
\end{eqnarray*}](img51.png)