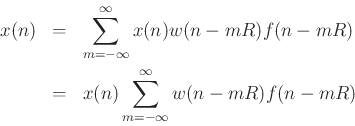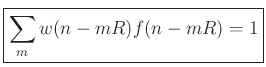Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The sequence of operations in a WOLA processor can be expressed as
follows:
- Extract the
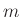 th windowed frame of data
th windowed frame of data
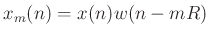 ,
,
 (assuming a length
(assuming a length 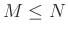 causal window
causal window 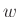 and hop
size
and hop
size  ).
).
- Take an FFT of the
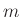 th frame translated to time zero,
th frame translated to time zero,
 , to produce the
, to produce the 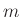 th spectral frame
th spectral frame
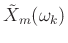 ,
,
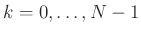 .
.
- Process
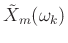 as desired to produce
as desired to produce
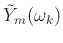 .
.
- Inverse FFT
 to produce
to produce
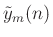 ,
,
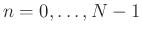 .
.
- Apply a synthesis window
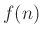 to
to
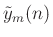 to yield a
weighted output frame
to yield a
weighted output frame
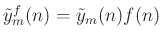 ,
,
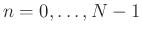 .
.
- Translate the
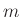 th output frame to time
th output frame to time 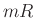 as
as
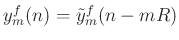 and add to the accumulated output signal
and add to the accumulated output signal 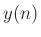 .
.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
[Comment on this page via email]