Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
- Take into account shear and lateral inertia effects
- Transverse motion still constrained to lie in one perpendicular direction
- Plane subsections remain plane, but no longer parallel to the normal direction:
- New degree of freedom,
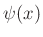 (in addition to
(in addition to 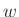 .
.
Timoshenko's Equations
- Dependent Variables:
- New material parameters:
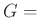 shear modulus
shear modulus
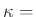 ``Timoshenko coefficient'' (geometrical)
``Timoshenko coefficient'' (geometrical)
Timoshenko's Equations Cont'd.
System:
with
- A symmetric hyperbolic system (bounded velocities)
- A pair of antisymmetrically coupled lossless transmission lines
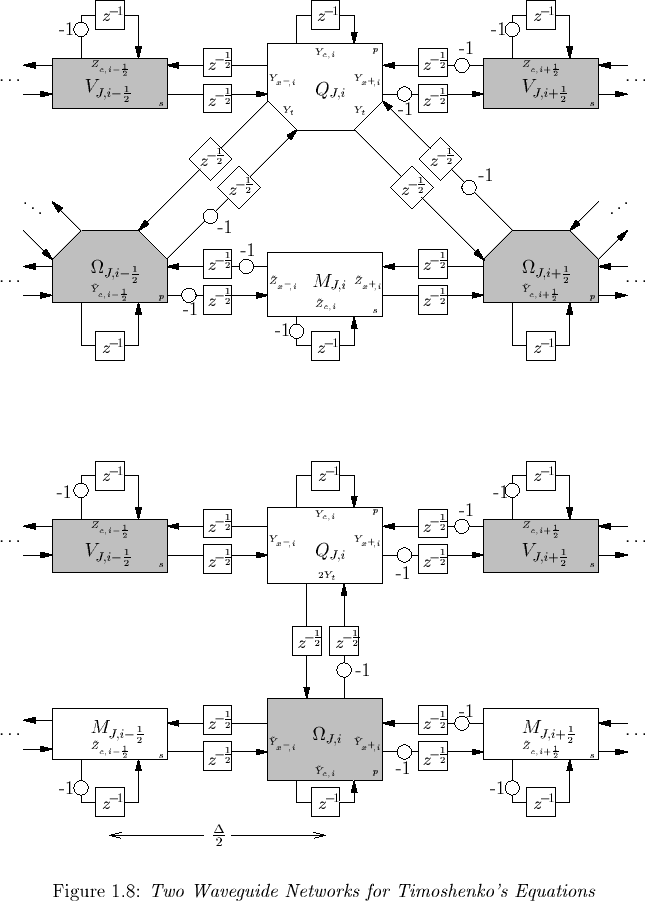
Networks for Timoshenko's Equations
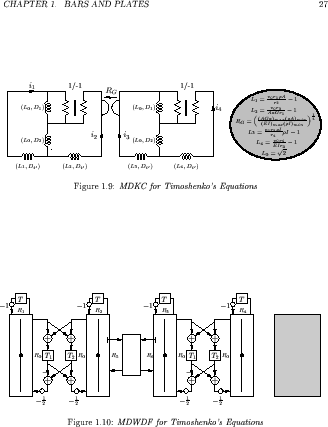
Multidimensional Circuit and Wave Digital Network for Timoshenko's Equations
Stability Condition for Waveguide Network for Timoshenko System
The maximum speeds of the Timoshenko Beam are
Stability conditions for the staggered waveguide mesh (TLM) are:
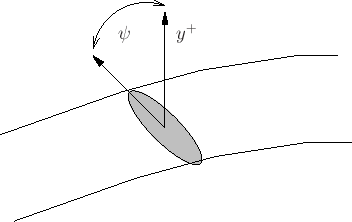
Also: A maximum permissible time-step (independent of 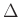 )
Aproaches CFL bound as
)
Aproaches CFL bound as
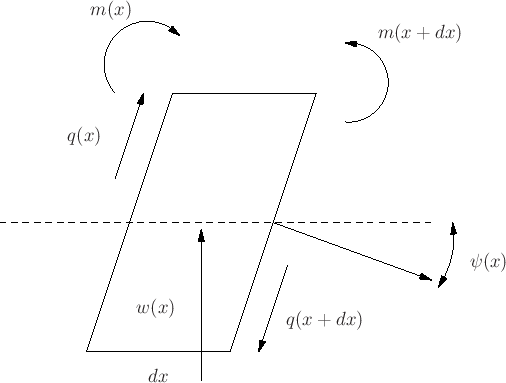
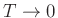 .
.
- Stability bound is complicated by the staggering (in contrast to the transmission line case)
- Fix: Can make stability bound optimal by introducing vector travelling waves
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Meshes.pdf
Download Meshes_2up.pdf
Download Meshes_4up.pdf


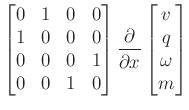

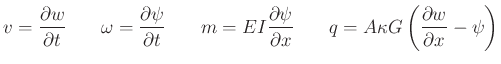
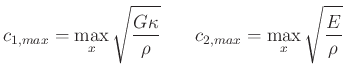
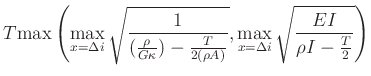
![]() )
Aproaches CFL bound as
)
Aproaches CFL bound as
![]() .
.