Mass-Spring Oscillator Analysis, Continued

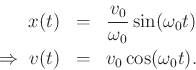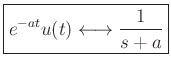
We can quickly verify that

$$\zbox{e^{-at}u(t) \longleftrightarrow \frac{1}{s+a}}$$

where $u(t)$ is the Heaviside unit step function which steps from 0 to 1 at time 0 .

By linearity, the solution for the motion of the mass is

$$\begin{eqnarray*} x(t) &=& re^{-j{\omega_0}t} + \overline{r}e^{j{\omega_0}t} = 2\mbox{re}\left\{re^{-j{\omega_0}t}\right\} = 2R_r\cos({\omega_0}t - \theta_r)\\ &=& \frac{\sqrt{v^2_0 + {\omega_0}^2 x^2_0}}{{\omega_0}} \cos\left[{\omega_0}t - \tan^{-1}\left(\frac{v_0}{{\omega_0}x_0}\right)\right] \end{eqnarray*}$$

If the initial velocity is zero ($v_0=0$ ), the above formula reduces to $x(t) = x_0\cos({\omega_0}t)$ and the mass simply oscillates sinusoidally at frequency ${\omega_0}= \sqrt{k/m}$ , starting from its initial position $x_0$ . If instead the initial position is $x_0=0$ , we obtain

$$\begin{eqnarray*} x(t) &=& \frac{v_0}{{\omega_0}}\sin({\omega_0}t)\\ \;\Rightarrow\; v(t) &=& v_0\cos({\omega_0}t). \end{eqnarray*}$$