Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The Laplace transform is a linear operator:
Proof: Let
where 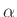 and
and 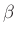 are real or complex constants. Then
are real or complex constants. Then
Thus, linearity of the Laplace transform follows immediately from
linearity of integration
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Laplace.pdf
Download Laplace_2up.pdf
Download Laplace_4up.pdf
![\begin{eqnarray*}
W(s) &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& {\cal L}_s\{w\} \mathrel{\stackrel{\mathrm{\Delta}}{=}}{\cal L}_s\{\alpha x(t) + \beta y(t)\}\\ [10pt]
&\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \int_0^\infty \left[\alpha x(t) + \beta y(t)\right] e^{-st} dt\\ [10pt]
&=& \alpha \int_0^\infty x(t) e^{-st} dt
+ \beta \int_0^\infty y(t) e^{-st} dt\\ [5pt]
&\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \alpha X(s) + \beta Y(s).
\end{eqnarray*}](img32.png)