Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
If the applied external force 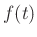 is zero, we obtain
is zero, we obtain
Since 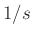 is the Laplace transform of the Heaviside unit-step function
is the Laplace transform of the Heaviside unit-step function
we find that the position of the mass 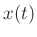 is given for all time by
is given for all time by
- A nonzero initial position
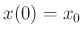 and zero
initial velocity
and zero
initial velocity 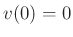 results in
results in 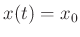 for all
for all 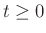 (mass ``just sits there'')
(mass ``just sits there'')
- Similarly, any initial velocity
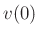 is integrated with
respect to time (mass moves forever at initial velocity)
is integrated with
respect to time (mass moves forever at initial velocity)
In summary, we used the Laplace transform to solve for the motion of a
simple physical system (an ideal mass) in response to initial
conditions (no external driving forces).
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Laplace.pdf
Download Laplace_2up.pdf
Download Laplace_4up.pdf
![]() is zero, we obtain
is zero, we obtain
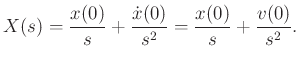
![$\displaystyle u(t)\mathrel{\stackrel{\mathrm{\Delta}}{=}}\left\{\begin{array}{ll}
0, & t<0 \\ [5pt]
1, & t\ge 0 \\
\end{array} \right.,
$](img54.png)