Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Note that in the electrical equivalent circuit
From Newton's second law of motion ``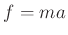 '', we have
'', we have
Taking the unilateral Laplace transform and applying the
differentiation theorem twice yields
Thus, given
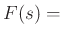 Laplace transform of the driving force
Laplace transform of the driving force 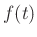 ,
,
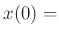 initial mass position, and
initial mass position, and
-
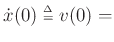 initial mass velocity,
initial mass velocity,
we can solve algebraically for 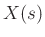 , the Laplace transform of the
mass position for all
, the Laplace transform of the
mass position for all 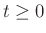
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Laplace.pdf
Download Laplace_2up.pdf
Download Laplace_4up.pdf
![]() '', we have
'', we have
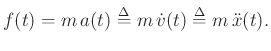
![\begin{eqnarray*}
F(s) &=& m\,{\cal L}_s\{{\ddot x}\}\\
&=& m\left[\,s {\cal L}_s\{{\dot x}\} - {\dot x}(0)\right]\\
&=& m\left\{\,s \left[s\,X(s) - x(0)\right] - {\dot x}(0)\right\}\\
&=& m\left[s^2\,X(s) - s\,x(0) - {\dot x}(0)\right].
\end{eqnarray*}](img46.png)