Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The differentiation theorem for Laplace transforms:
where
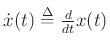 , and
, and 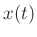 is any
differentiable function that approaches zero as
is any
differentiable function that approaches zero as 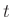 goes to infinity.
goes to infinity.
Operator notation:
Proof: Immediate from integration by parts:
since
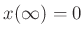 by assumption
by assumption
Corollary: Integration Theorem:
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Laplace.pdf
Download Laplace_2up.pdf
Download Laplace_4up.pdf
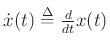 , and
, and ![\begin{eqnarray*}
{\cal L}_{s}\{{\dot x}\} &\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \int_{0}^\infty {\dot x}(t) e^{-s t} dt\\ [10pt]
&=& \left. x(t)e^{-s t}\right\vert _{0}^{\infty} -
\int_{0}^\infty x(t) (-s)e^{-s t} dt\\ [10pt]
&=& s X(s) - x(0)
\end{eqnarray*}](img37.png)
![]() by assumption
by assumption