One Sine and One Cosine
(``Phase Quadrature'' Case)
All Four Resolutions Overlaid

• Same plots as on previous page, just overlaid
• Peak locations are biased in under-resolved cases, both in amplitude and frequency

The preceding figures suggest that, for a rectangular window of length $M$ , two sinusoids can be most reliably resolved when they are separated in frequency by a full main-lobe width:

$$\zbox{\Delta\omega\geq 2\Omega_M} \qquad \left(\Omega_M \isdef \frac{2\pi}{M}\right)$$

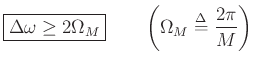
This implies there must be at least two full cycles of the difference-frequency under the window.

We'll see later that this is an overly conservative requirement--a more careful study reveals that $1.44$ cycles is sufficient for the rectangular window.