Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Theorem:
Proof: Let 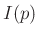 denote the integral. Then
denote the integral. Then
where we needed
re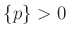 to have
to have
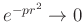 as
as
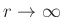 . Thus,
. Thus,
as claimed.
Subsections
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
[Comment on this page via email]
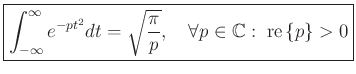
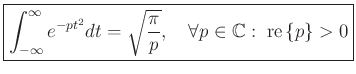
![]() denote the integral. Then
denote the integral. Then
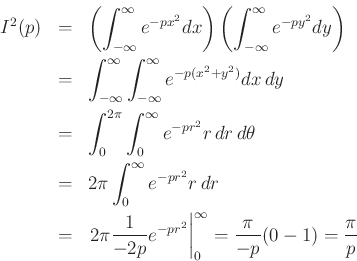
![]() to have
to have
![]() as
as
![]() . Thus,
. Thus,