STFT Filterbank

The STFT

$$X_m(\omega_k) = \sum_{n=-\infty}^\infty [ x(n)e^{-j\omega_k n}] w(n-mR)$$

may be computed by the following operations:

• Demodulate 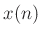$x(n)$ to get $x_k(n) \mathrel{\stackrel{\Delta}{=}}e^{-j\omega_k n}x(n)$
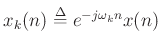
  • multiplication by 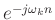$e^{-j\omega_k n}$ shifts 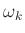$\omega_k$ down to dc
• Next, convolve with $\tilde{w}\mathrel{\stackrel{\Delta}{=}}\hbox{\sc Flip}(w)$
• Downsample by the (integer) factor $R$

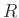
Thus, we can write

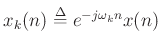
$$\begin{eqnarray*} X_m(\omega_k) = &=& \sum_{n=-\infty}^\infty [x(n)e^{-j\omega_kn}]\tilde{w}(mR-n) \\ &=& (x_k \ast \tilde{w})(mR) \hspace{1.2cm} (\tilde{w} \mathrel{\stackrel{\Delta}{=}}\hbox{\sc Flip}(w)) \end{eqnarray*}$$