Properties of the Bilinear Transform

The bilinear transform maps an $s$ -plane transfer function $H_a(s)$ to a $z$ -plane transfer function:

$$\zbox{H_d(z) \;\mathrel{\stackrel{\mathrm{\Delta}}{=}}\;H_a\left(c\frac{1-z^{-1}}{1+z^{-1}}\right)}$$

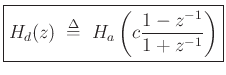
We can observe the following properties of the bilinear transform:

• Analog dc ($s=0$ ) maps to digital dc ($z=1$ )

• Infinite analog frequency ($s=\infty$ ) maps to the maximum digital frequency ($z=-1$ )

• The entire $j\omega$ axis in the $s$ plane (where $s\mathrel{\stackrel{\scriptscriptstyle\mathrm{\Delta}}{\scriptstyle=}}\sigma+j\omega$ ) is mapped exactly once around the unit circle in the $z$ plane (rather than summing around it infinitely many times, or ``aliasing'' as it does in ordinary sampling)

• Stability is preserved (when $c$ is real and positive)

• Order of the transfer function is preserved

• Choose $c$ to map any particular finite frequency (such as a resonance frequency) from the $j\omega_a$ axis in the $s$ plane to a particular desired location on the unit circle $e^{j\omega_d}$ in the $z$ plane. Other frequencies are ``warped''.

Bilinear Transform of Force-Driven Mass

We have, from $f=m\dot v\;\leftrightarrow\;F(s)=ms\,V(s)$ ,

$$V(s) = \frac{1}{ms}F(s)$$

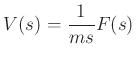
Setting $s=(2/T)(1-z^{-1})/(1+z^{-1})$ according to the bilinear transform yields

$$V_d(z) = \frac{T}{2m}\frac{1+z^{-1}}{1-z^{-1}}F_d(z)$$

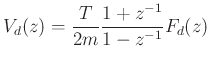
where we defined

$$\begin{eqnarray*} F_d(z) &=& F\left(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\right)\\ [10pt] V_d(z) &=& V\left(\frac{2}{T}\frac{1-z^{-1}}{1+z^{-1}}\right) \end{eqnarray*}$$

The resulting finite-difference scheme is then

$$v_d(n) - v_d(n-1) = \frac{T}{2m}\left[f_d(n)+f_d(n-1)\right]$$

i.e.,

$$v_d(n) = v_d(n-1) + \frac{T}{2m}\left[f_d(n)+f_d(n-1)\right]$$

We see that this is the same as the backward Euler scheme plus a new term $(T/2m) f_d(n-1)$ .