Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
In general, (finite-order) allpass filters can be written as
where
- The polynomial
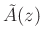 can be obtained by reversing the order of the
coefficients in
can be obtained by reversing the order of the
coefficients in 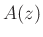 and conjugating them
and conjugating them
- The problem of dispersion filter design is typically formulated
as an allpass-filter design problem
Next |
Prev |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Delay.pdf
Download Delay_2up.pdf
Download Delay_4up.pdf
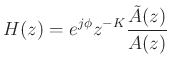
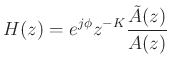
![\begin{eqnarray*}
A(z) &=& 1 + a_1 z^{-1}+ a_2 z^{-2} + \cdots + a_N z^{-N}\\ [10pt]
\tilde{A}(z)&\mathrel{\stackrel{\mathrm{\Delta}}{=}}& z^{-N}\overline{A}(z^{-1})\\ [10pt]
&\mathrel{\stackrel{\mathrm{\Delta}}{=}}& \overline{a}_N + \overline{a}_{N-1} z^{-1}+ \cdots + \overline{a}_1 z^{-(N-1)} + \cdots + z^{-N}
\end{eqnarray*}](img72.png)