Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
The substitution
in any transfer function contracts all poles by the factor 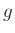 .
.
Example (delay line):
Thus, the contraction factor 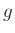 can be interpreted as the per-sample
propagation loss factor.
can be interpreted as the per-sample
propagation loss factor.
Frequency-Dependent Losses:
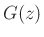 can be considered the filtering per sample in the
propagation medium. A lossy delay line is thus described by
can be considered the filtering per sample in the
propagation medium. A lossy delay line is thus described by
in the frequency domain, and iterated convolution
in the time domain
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Delay.pdf
Download Delay_2up.pdf
Download Delay_4up.pdf
