Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
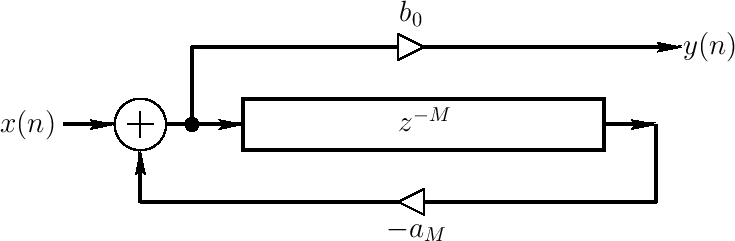
Direct-Form-II Difference Equation (see figure):
Direct-Form-I Difference Equation
(commute gain  to the input):
to the input):
Transfer Function
Frequency Response
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download Delay.pdf
Download Delay_2up.pdf
Download Delay_4up.pdf


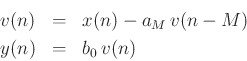
![]() to the input):
to the input):

