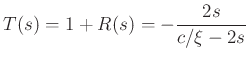Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Wave impedance at frequency 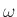 rad/sec in a converging cone:
rad/sec in a converging cone:
where
In the limit as
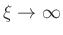 ,
,
Reflectance of the conical cap, seen from cylinder:
Transmittance to the right:
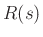 and
and 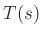 are first-order transfer functions,
each having a single real pole at
are first-order transfer functions,
each having a single real pole at
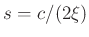
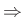 unstable
unstable
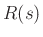 and
and 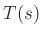 identical from
left and right given no wavefront area discontinuity.
identical from
left and right given no wavefront area discontinuity.
Next |
Prev |
Up |
Top
|
JOS Index |
JOS Pubs |
JOS Home |
Search
Download ConicalModeling.pdf
Download ConicalModeling_2up.pdf
Download ConicalModeling_4up.pdf
![]() rad/sec in a converging cone:
rad/sec in a converging cone:
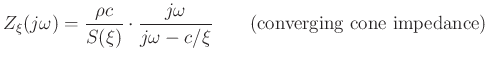
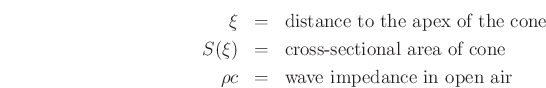
![]() ,
,