
[Introduction | Algorithms | Results | Conclusion | Reference | Appendix ]
An automatic face morphing algorithm is proposed. The algorithm automatically extracts feature points on the face, and based on these feature points images are partitioned and face morphing is performed. The algorithm has been used to generate morphing between images of faces of different people as well as between different images of the face of an individual. The results of both inter- and intra-personal morphing are subjectively satisfactory.
Morphing applications are everywhere. Hollywood film makers use novel morphing technologies to generate special effects, and Disney uses morphing to speed up the production of cartoons. Among so many morphing applications, we are specifically interested in face morphing because we believe face morphing should have much more important applications than other classes of morphing.
To do face morphing, feature points are usually specified manually in animation industries [2]. To alleviate the demand for human power, M. Biesel [1] proposed an algorithm within Bayesian framework to do automatic face morphing. However, his approach involved computation of 3N dimensional probability density function, N being the number of pixels of the image, and we thought the approach was too much computation-demanding.
Therefore, we would like to investigate how feature finding algorithms can help us achieve automatic face morphing. Within the scope of this project, we built up a prototypical automatic animation generator that can take an arbitrary pair of facial images and generate morphing between them.
Outline of our Procedures
Our algorithm consists of a feature finder and a
face morpher. The following figure illustrates our procedures.

The details for the implementations will be discussed in the following paragraphs.
Pre-Processing
When getting an image containing human faces, it is always better to do some pre-processing such like removing the noisy backgrounds, clipping to get a proper facial image, and scaling the image to a reasonable size. So far we have been doing the pre-processing by hand because we would otherwise need to implement a face-finding algorithm. Due to time-limitation, we did not study automatic face finder.
Feature Finding
Our goal was to find 4 major feature points, namely
the two eyes, and the two end-points of the mouth. Within the scope
of this project, we developed an eye-finding algorithm that successfully
detect eyes at 84% rate. Based on eye-finding result, we can then
find the mouth and hence the end-points of it by heuristic approach.
1. Eye-finding
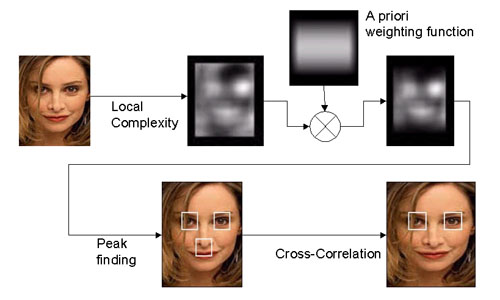
The figure below illustrates our eye-finding algorithm.
We assume that the eyes are more complicated than other parts of the face.
Therefore, we first compute the complexity map of the facial image by sliding
a fixed-size frame and measuring the complexity within the frame in a "total
variation" sense. Total variation is defined as the sum of difference
of the intensity of each pair of adjacent pixels. Then, we multiply
the complexity map by a weighting function that is set a priori.
The weighting function specifies how likely we can find eyes on the face
if we don't have any prior information about it. Afterwards, we find
the three highest peaks in the weighted complexity map, and then we decide
which two of the three peaks, which are our candidates of eyes, really
correspond to the eyes. The decision is based on the similarity between
each pair of the candidates, and based on the location where these candidates
turn out to be. The similarity is measured in the correlation-coefficient
sense, instead of the area inner-product sense, in order to eliminate the
contribution from variation in illumination.
2. Mouth-finding
After finding the eyes, we can specify the mouth
as the red-most region below the eyes. The red-ness function is given
by
|
Redness = ( R > G * 1.2 ? ) * ( R > Rth ? ) * { R / (G + epsilon ) } |

Image Partitioning
Our feature finder can give us the positions of the eyes and the ending points of the mouth, so we get 4 feature points. Beside these facial features, the edges of the face also need to be carefully considered in the morphing algorithm. If the face edges do not match well in the morphing process, the morphed image will look strange on the face edges. We generate 6 more feature points around the face edge, which are the intersection points of the extension line of the first 4 facial feature points with the face edges. Hence, totally we have 10 feature points for each face. In the following figure, the white dots correspond to the feature points.

Based on these 10 feature points, our face-morpher partitions each photo into 16 non-overlapping triangular or quadrangular regions. The partition is illustrated in the following two pictures. Ideally, if we could detect more feature points automatically, we would be able to partitioned the image into finer meshes, and the morphing result would have been even better.
Image 1
Image 2
 __________
__________
Since the feature points of images 1 and 2 are, generally
speaking, at different positions, when doing morphing between images, the
images have to be warped such that their feature points are matched.
Otherwise, the morphed image will have four eyes, two mouths, and so forth.
It will be very strange and unpleasant that way.
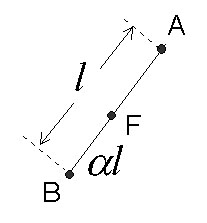
Suppose we would like to make an intermediate image
between images 1 and 2, and the weightings for images 1 and 2 are alpha
and (1-alpha), respectively. For a feature point A in image 1, and the
corresponding feature point B in image 2, we are using linear interpolation
to generate the position of the new feature point F:
![]()
The new feature point F is used to construct a point
set which partitions the image in another way different from images 1 and
2. Images 1 and 2 are warped such that their feature points are moved to
the same new feature points, and thus their feature points are matched.
In the warping process, coordinate transformations are performed for each
of the 16 regions respectively.
Coordinate Transformations
There exist many coordinate transformations for the mapping between two triangles or between two quadrangles. We used affine and bilinear transformations for the triangles and quadrangles, respectively. Besides, bilinear interpolation is performed in pixel sense.
1. Affine Transformation
Suppose we have two triangles ABC and DEF. An affine transformation is a linear mapping from one triangle to another. For every pixel p within triangle ABC, assume the position of p is a linear combination of A, B, and C vectors. The transformation is given by the following equations,

Here, there are two unknowns, Lambda1 and Lambda2, and two equations for each of the two dimensions. Consequently, Lambda1 and Lambda2 can be solved, and they are used to obtain q. I.e., the affine transformation is a one-to-one mapping between two triangles.
2. Bilinear Transformation

Suppose we have two quadrangles ABCD and EFGH. The
Bilinear transformation is a mapping from one quadrangle to another.
For every pixel p within quadrangle ABCD, assume that the position of p
is a linear combination of vectors A, B, C, and D. Bilinear transformation
is given by the following equations,
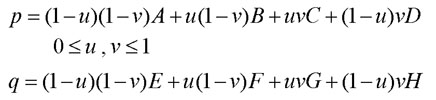
There are two unknowns u and v. Because this is a
2D problem, we have 2 equations. So, u and v can be solved, and they are
used to obtain q. Again, the Bilinear transformation is a one-to-one
mapping for two quadrangles.
Cross-Dissolving
After performing coordinate transformations for each of the two facial images, the feature points of these images are matched. i.e., the left eye in one image will be at the same position as the left eye in the other image. To complete face morphing, we need to do cross-dissolving as the coordinate transforms are taking place. Cross-dissolving is described by the following equation,

where A,B are the pair of images, and C is the morphing result.
This operation is performed pixel by pixel, and each
of the color components RGB are dealt with individually.
The following example demonstrates a typical morphing process.
1. The original images of Ally and Lion, scaled to the same size. Please note that the distance between the eyes and the mouth is significantly longer in the lion's picture than in Ally's picture.
 __________
__________
2. Perform coordinate transformations on the partitioned images to match the feature points of these two images. Here, we are matching the eyes and the mouths for these two images. We can find that Ally's face becomes longer, and the lion's face becomes shorter.
 __________
__________
3. Cross-dissolve the two images to generate a new image.
The morph result looks like a combination of these two wrapped faces.
The new face has two eyes and one mouth, and it possesses the features
from both Ally's and the lion's faces.
_______________
1. Feature-finding results
We first fine-tuned the parameters of the eye-finder
so that it can successfully detect the eyes in the photos of 13 different
celebrities. Afterwards, we evaluated the performance of the eye-finder
by applying it to 160 of properly scaled photos of 1999-2000
EE new graduate students at Stanford. The eye-finder successfully
detected both eyes from 113 of the 160 students, one of the two eyes of
42 students, and none of the two eyes of 5 students. Being able to
detect 268 out of 320 eyes, the eye-finder had a detection rate of 84%.
The following pictures are some of the successful
examples. Note that in the training set, some faces in the photos
were either tilting or not looking into the front directions, but our eye-finder
was still able to correctly detect the eyes. Also note that the training
set has people of different skin-colors and of both sexes.

Among those of the pictures for which the eye-finder
failed, all sorts of other features such like ears, mouths, noses, rims
of glasses, etc, were detected instead. Also, the eye-detection rate
for people wearing glasses are lower than people not wearing glasses.
Below we illustrate some examples of wrong detection.
 |
 |
 |
2. Morphing Results
(1) Morphing between faces of different people
Here are some non-animated morphing examples. We performed face morphing for several different cases
- human and animal (lion)
- man and man
- man and woman
In the following, the very left and very right images of each row are original images, and the intermediate ones are synthesized morphed images.




(2) Morphing between different images of the same person
The following are morphing examples for the faces of a person with different
expressions or poses.
We want to interpolate the intermediate expressions or poses by morphing.
Serious
<===
===> Smiling

Looking forward <===
===> Facing another way
Happy
<===
===> Angry

Straight
<===
===> Swinging head

Animation of all the above examples can be found here
IV.
Conclusion
An automatic face morphing algorithm is proposed.
The algorithm consists of a feature finder followed by a face-morpher that
utilizes affine and bilinear coordinate transforms.
We believe that feature extraction is the key technique
toward building entirely automatic face morphing algorithms. Moreover,
we believe that the eyes are the most important features of human faces.
Therefore, in this project we developed an eye-finder based on the idea
that eyes are, generally speaking, more complicated than the rest of the
face. We hence achieved an 84% of eye detection rate. Also,
we proposed red-ness, green-ness and blue-ness function and illustrated
how we would be able to find the mouth based on these functions.
We demonstrated that a hybrid image of two human
faces can be generated by morphing, and the hybrid face we generated indeed
resembles each of the two "parent" faces. Also, we demonstrated that
face morphing algorithms can help generate animation.
Ideally speaking, the more feature points we can
specify on the faces, the better morphing results we can obtain. If we
can specify all the important facial features such as the eyes, the eyebrows,
the nose, the edge points of the mouth, the ears, and some specific points
of the hair, we are confident that we can generate very smooth and realistically
looking morphing from one image to another.
[1] Martin Bichsel, "Automatic Interpolation and Recognition of Face
Images by Morphing", proceedings of the 2nd
international conference on automatic face and gesture recognition, pp128-135
[2] Jonas Gomes et al. "Warping and morphing of graphical objects ",
Morgan Kaufmann Publishers (1999).