


Next: Bayesian Framework Application
Up: BAYESIAN TWO SOURCE MODELING
Previous: DUET and DASSS Review
As suggested above, the DASSS data produced by equation 4
may in fact reveal which two sources are active at a
particular point in time-frequency space if exactly two sources
are active. This is very useful information, because once the
active sources are known, they may be demixed by solving for 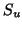 and
and 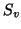 in:
in:
which follows directly from equations 1 and 2 when
only two sources are active.
Formally, we express the two most likely sources given some DUET
or DASSS data 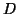 as those maximizing
as those maximizing 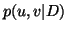 . Applying
Bayes' rule, we can express this as
. Applying
Bayes' rule, we can express this as
We can see by inspection of equations 9
through 11 that the STFT frequency under
consideration, 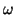 , affects DASSS data
, affects DASSS data 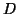 (the
(the 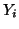 values). So, we are mindful that the problem is a different one
for each of the frequency values
values). So, we are mindful that the problem is a different one
for each of the frequency values 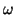 under consideration.
Since
under consideration.
Since  is not a function of
is not a function of 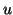 or
or 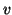 , it is possible to
discard it from the maximization (though we may wish to use it
later if a confidence measure is sought). The quantity
, it is possible to
discard it from the maximization (though we may wish to use it
later if a confidence measure is sought). The quantity  is
largely estimated with musical knowledge. For example we may know
that the clarinet (source
is
largely estimated with musical knowledge. For example we may know
that the clarinet (source 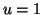 for example) tends to play at the
same time as and less loudly than the violin (say, source
for example) tends to play at the
same time as and less loudly than the violin (say, source 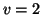 ),
whose frequency components tend to be at harmonics of frequencies
above 200 Hz, and rarely throughout time. Though very useful, such
information is not within our current signal processing interest,
and is not considered now. (For now, we will treat all
),
whose frequency components tend to be at harmonics of frequencies
above 200 Hz, and rarely throughout time. Though very useful, such
information is not within our current signal processing interest,
and is not considered now. (For now, we will treat all  as
equally likely.)
We are left, then, to consider
as
equally likely.)
We are left, then, to consider 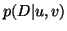 for each
for each 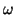 , the
probability that particular DASSS data is produced when sources
, the
probability that particular DASSS data is produced when sources
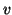 and
and 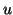 (but no others) are active at frequency
(but no others) are active at frequency 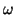 . To
this end, we next explicitly return to the distributions suggested
by equations 9 through 11. By doing so, we
identify the necessary values of
. To
this end, we next explicitly return to the distributions suggested
by equations 9 through 11. By doing so, we
identify the necessary values of 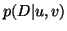 where
where 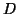 represents
DASS scores
represents
DASS scores 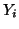 .
.



Next: Bayesian Framework Application
Up: BAYESIAN TWO SOURCE MODELING
Previous: DUET and DASSS Review
Aaron S. Master
2003-10-30
![$\displaystyle \left[ \begin{array}{c} S_u \\ S_v \\ \end{array} \right]$](img49.png)
![$\displaystyle \left[ \begin{array}{cc} 1 & 1 \\
a_u e^{-j\omega\delta_u} & a_v...
...nd{array} \right]^{-1}
\left[ \begin{array}{c} X_1 \\ X_2 \end{array} \right],$](img50.png)