


Next: Bayesian Framework
Up: BAYESIAN TWO SOURCE MODELING
Previous: Introduction
We first review the DUET
system [4,5,1]
of Scott Rickard and other authors. The DUET system performs
sound source separation of 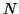 sources from two channels, where
sources from two channels, where
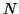 is in general greater than two. The DUET system assumes the
following STFT domain linear mixing model for sources
is in general greater than two. The DUET system assumes the
following STFT domain linear mixing model for sources 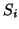 in
left channel
in
left channel 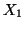 and right channel
and right channel 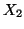 :
:
where 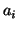 represents the scale parameter and
represents the scale parameter and 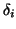 represents the delay parameter, each from the left to right
channel, for some source
represents the delay parameter, each from the left to right
channel, for some source 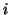 . We refer to
. We refer to 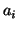 and
and 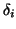 together as the mixing parameters for a given source
together as the mixing parameters for a given source 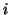 .
By assuming that only one source at a time is active in
time-frequency space - a near-realistic assumption for
independent speech sources - we may estimate the mixing
parameters for a particular time-frequency point via:
.
By assuming that only one source at a time is active in
time-frequency space - a near-realistic assumption for
independent speech sources - we may estimate the mixing
parameters for a particular time-frequency point via:
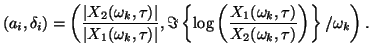 |
|
|
(3) |
After collecting many such estimates, the DUET system prepares a
two-dimensional histogram whose peaks in
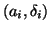 space
should reveal the mixing parameters for each of the
space
should reveal the mixing parameters for each of the 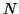 sources.
To demix the sources, DUET considers the set of parameter
estimates a second time after the source mixing parameters are
estimated from the histogram. It then assigns each point in
time-frequency space to the source whose mixing parameters are
closest to that estimated for the time-frequency point. To do
this, a variety of matching schemes may be used. We have
presented delay and scale subtraction scoring
(DASSS) [2], which is similar to a method presented
recently by the original DUET authors in [1].
In DASSS, we define a set of functions
sources.
To demix the sources, DUET considers the set of parameter
estimates a second time after the source mixing parameters are
estimated from the histogram. It then assigns each point in
time-frequency space to the source whose mixing parameters are
closest to that estimated for the time-frequency point. To do
this, a variety of matching schemes may be used. We have
presented delay and scale subtraction scoring
(DASSS) [2], which is similar to a method presented
recently by the original DUET authors in [1].
In DASSS, we define a set of functions 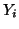 such that:
such that:
and the mixing parameters are always treated as known quantities.
If in fact exactly one source, 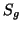 , is active at a given
frequency bin in a given frame, it may be shown that our model
predicts:
, is active at a given
frequency bin in a given frame, it may be shown that our model
predicts:
where
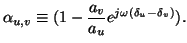 |
|
|
(8) |
We now observe that we may similarly predict the DASSS function
values 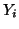 when two sources
when two sources 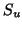 and
and 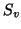 are active:
are active:
We now make an important observation. If we know how 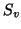 and
and
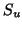 are distributed, we then know how
are distributed, we then know how 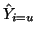 ,
,
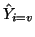 , and
, and
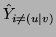 are distributed. (In
general, we will see that distributions on
are distributed. (In
general, we will see that distributions on 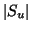 and
and 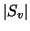 may
be practically estimated from knowledge about a musical or speech
source, such as its range and loudness. Distributions on
may
be practically estimated from knowledge about a musical or speech
source, such as its range and loudness. Distributions on 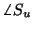 and
and 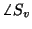 are not informative, and thus we will use
the set
are not informative, and thus we will use
the set 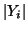 ,
,
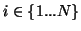 rather than the sets
rather than the sets 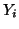 or
or
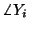 as our DASSS data.) Below, we will exploit our
knowledge of the DASSS data in a Bayesian context to determine if
(and which) two sources are most likely active.
Much as we know how the DASSS data
as our DASSS data.) Below, we will exploit our
knowledge of the DASSS data in a Bayesian context to determine if
(and which) two sources are most likely active.
Much as we know how the DASSS data 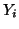 functions will behave for
the two source case, it may also be shown [6] that we
can predict the values for the DUET data given by equation
3 in the same case. It is not practical, however, to
exploit this data, as logistics and computation quickly become
prohibitive [6]. We therefore focus our efforts on
DASSS data below.
functions will behave for
the two source case, it may also be shown [6] that we
can predict the values for the DUET data given by equation
3 in the same case. It is not practical, however, to
exploit this data, as logistics and computation quickly become
prohibitive [6]. We therefore focus our efforts on
DASSS data below.



Next: Bayesian Framework
Up: BAYESIAN TWO SOURCE MODELING
Previous: Introduction
Aaron S. Master
2003-10-30