


Next: DUET and DASSS Review
Up: BAYESIAN TWO SOURCE MODELING
Previous: BAYESIAN TWO SOURCE MODELING
Introduction
Sound source separation refers to the problem of
synthesizing 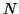 source signals given an
source signals given an 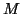 channel mixture of
those source signals. When there are fewer input mixtures than
sources to be separated (
channel mixture of
those source signals. When there are fewer input mixtures than
sources to be separated (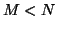 ), we have the degenerate
case. In the degenerate case, it is necessary to use prior
information about the source signals to perform demixing, because
of the ill-posed nature of the inverse mathematical problem.
We presently consider the two mixture degenerate case. In digital
audio, we frequently encounter this case, as many or most
currently available commercial digital recordings contain two
channels (stereo) but more than two instruments, voices, or other
sounds.
A variety of approaches to this and other degenerate problems have
been tried [3]. Each method exploits one or more
features of the sound sources, as they must do in order to be
successful. Such features include the sources' time-frequency
sparsity, their time-frequency independence, and their distinct
amplitude and delay characteristics between the mixtures. A brief
review of these techniques for the two source case is included
in [1].
We find that the DUET
system [4,5,1]
has achieved particularly convincing results, but can still be
improved. Specifically, we note that the system only works as
intended when in fact the sources are distinct in time-frequency
space. This is referred to as ``source sparsity'' although
non-overlap of sources is also required. This is because
co-occurring sparse sources cannot be separated. In performance of
tonal Western music, sources are in general sparse because
instrumental ranges are finite and most compositions do not
require constant playing or singing throughout time. The sources,
however, are not in general independent, unless the ensemble is
without skill or the music requires that players sound notes in a
deliberately random fashion. The harmonic nature of Western music
exacerbates the problem, because harmonics whose fundamental
frequencies are in (possibly imperfectly) consonant relations will
overlap. Even in the case of dissonant or deliberately random
music, pitches are in general discretized to the 12-tone Western
scale, leading to overlap of some harmonics.
Given these facts, it is necessary that the DUET system be
modified if it is to deal with non-independent sources such as
those seen in music. Presently, we consider a method for the case
when exactly two unknown sources are present. This means that two
instruments or voices are sounding though we do not know a priori
if it is, for example, the bass and cello or cello and flute.
Clearly, this case is only an incremental improvement of the
current one-source-at-a-time system. However, in the cases of
musical trios or four speaker examples, the two-source assumption
is of great benefit.
To consider the benefit in the current approach, we first review
the DUET system and the related delay and scale subtraction
scoring (DASSS) [2], and explore how these models are
affected when two sources are present at the same point in
time-frequency space. In the third section, we consider how to
exploit the two-source system response in a Bayesian context.
Specifically, we develop a method for scoring the probability that
two particular sources are active given DASSS data. We conclude
with a musical example showing the efficacy of using Bayesian
Modeling of DASSS data rather than DUET for determining and
demixing two active sources.
), we have the degenerate
case. In the degenerate case, it is necessary to use prior
information about the source signals to perform demixing, because
of the ill-posed nature of the inverse mathematical problem.
We presently consider the two mixture degenerate case. In digital
audio, we frequently encounter this case, as many or most
currently available commercial digital recordings contain two
channels (stereo) but more than two instruments, voices, or other
sounds.
A variety of approaches to this and other degenerate problems have
been tried [3]. Each method exploits one or more
features of the sound sources, as they must do in order to be
successful. Such features include the sources' time-frequency
sparsity, their time-frequency independence, and their distinct
amplitude and delay characteristics between the mixtures. A brief
review of these techniques for the two source case is included
in [1].
We find that the DUET
system [4,5,1]
has achieved particularly convincing results, but can still be
improved. Specifically, we note that the system only works as
intended when in fact the sources are distinct in time-frequency
space. This is referred to as ``source sparsity'' although
non-overlap of sources is also required. This is because
co-occurring sparse sources cannot be separated. In performance of
tonal Western music, sources are in general sparse because
instrumental ranges are finite and most compositions do not
require constant playing or singing throughout time. The sources,
however, are not in general independent, unless the ensemble is
without skill or the music requires that players sound notes in a
deliberately random fashion. The harmonic nature of Western music
exacerbates the problem, because harmonics whose fundamental
frequencies are in (possibly imperfectly) consonant relations will
overlap. Even in the case of dissonant or deliberately random
music, pitches are in general discretized to the 12-tone Western
scale, leading to overlap of some harmonics.
Given these facts, it is necessary that the DUET system be
modified if it is to deal with non-independent sources such as
those seen in music. Presently, we consider a method for the case
when exactly two unknown sources are present. This means that two
instruments or voices are sounding though we do not know a priori
if it is, for example, the bass and cello or cello and flute.
Clearly, this case is only an incremental improvement of the
current one-source-at-a-time system. However, in the cases of
musical trios or four speaker examples, the two-source assumption
is of great benefit.
To consider the benefit in the current approach, we first review
the DUET system and the related delay and scale subtraction
scoring (DASSS) [2], and explore how these models are
affected when two sources are present at the same point in
time-frequency space. In the third section, we consider how to
exploit the two-source system response in a Bayesian context.
Specifically, we develop a method for scoring the probability that
two particular sources are active given DASSS data. We conclude
with a musical example showing the efficacy of using Bayesian
Modeling of DASSS data rather than DUET for determining and
demixing two active sources.



Next: DUET and DASSS Review
Up: BAYESIAN TWO SOURCE MODELING
Previous: BAYESIAN TWO SOURCE MODELING
Aaron S. Master
2003-10-30