Next |
Prev |
Up |
Top
|
REALSIMPLE Top
The speed of sound is the same in an acoustic tube as in the open air. In this
section, we will explain some formulae relating to this quantity.
When sound propagates in an acoustic tube, there are two key quantities we need
to keep track of:
- the pressure in the tube
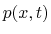 at a given point
at a given point  along the tube's
length and time
along the tube's
length and time 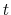 , measured in Pa or N/m, and
, measured in Pa or N/m, and
- the volume velocity in the tube
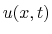 at the same point
at the same point  along the
tube's length and time
along the
tube's length and time 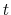 , measured in
, measured in 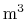 /s.
/s.
It may be shown that the two quantities above obey the wave equation, and thus
each quantity may be decomposed into right-traveling and left-traveling wave components as
 |
(1) |
and
 |
(2) |
as discussed in the traveling waves laboratory assignment.
What the equations above state is
that any pressure and volume velocity functions that may realistically
exist in the tube can each be decomposed into a pair of simpler functions, one
a waveform traveling to the right (e.g., 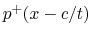 ),
and the other a
waveform traveling to the left (e.g.,
),
and the other a
waveform traveling to the left (e.g., 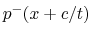 ). The speed at
which these waveforms travel,
). The speed at
which these waveforms travel,  , is the speed of sound in the tube.
, is the speed of sound in the tube.
As mentioned earlier, the speed of sound
 in an air-filled
acoustic tube is the same as the speed of sound in the open air. As a result,
the radius of the tube has no effect on
in an air-filled
acoustic tube is the same as the speed of sound in the open air. As a result,
the radius of the tube has no effect on
 . In order to derive a
formula for
. In order to derive a
formula for
 , it may first be shown that, based on
classical fluid mechanics,
, it may first be shown that, based on
classical fluid mechanics,
 |
(3) |
where 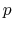 denotes the fluid pressure, and
denotes the fluid pressure, and  denotes the fluid density.
denotes the fluid density.
Next we need to note an important and non-obvious property about sound
propagation. It turns out that sound propagates approximately
adiabatically. What
this means is that as the fluid pressure fluctuates rapidly during sound
propagation, the temperature of the fluid also fluctuates, but no heat is
gained or lost due to this fluctuation. If heat were gained or lost, we would
not have an adiabatic process. The key equation describing an adiabatic
process relates pressure 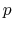 and density
and density  as follows:
as follows:
 |
(4) |
where  is a constant, and
is a constant, and  is the adiabatic index. For diatomic
gases such as air,
is the adiabatic index. For diatomic
gases such as air,
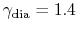 .
Using the equations above, it may be
shown that
.
Using the equations above, it may be
shown that
 |
(5) |
Next, the ideal gas law (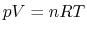 ) may be used to derive the following
formula:
) may be used to derive the following
formula:
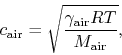 |
(6) |
where 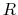 is the universal gas constant (
is the universal gas constant ( J/[mol K]),
J/[mol K]), 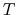 is the
absolute temperature in degrees Kelvin, and
is the
absolute temperature in degrees Kelvin, and  is the molar mass of the fluid
(in kg/mol). For dry air,
is the molar mass of the fluid
(in kg/mol). For dry air, 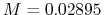 kg/mol.
kg/mol.
Subsections
Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Download vir_tube.pdf
![]() in an air-filled
acoustic tube is the same as the speed of sound in the open air. As a result,
the radius of the tube has no effect on
in an air-filled
acoustic tube is the same as the speed of sound in the open air. As a result,
the radius of the tube has no effect on
![]() . In order to derive a
formula for
. In order to derive a
formula for
![]() , it may first be shown that, based on
classical fluid mechanics,
, it may first be shown that, based on
classical fluid mechanics,
![]() and density
and density ![]() as follows:
as follows:
![]() ) may be used to derive the following
formula:
) may be used to derive the following
formula: