PID Control

We will use the simplified physical model of a plucked vibrating string as explained in the monochord laboratory assignment. Recall that as depicted in Figure 2, $m$ is the mass in kg, $K$ is the spring constant in N/m, and $R$ corresponds to friction and is measured in N/(m/s). This kind of friction may for instance be implemented using a viscous resistance. Since we are studying musical instruments, the decay time of the displaced mass-spring-damper system will be long enough that the vibration will be almost periodic. The system may be considered ``lightly damped'', which is the same as having $R$ be small. The $m$, $K$, and $R$ parameters could be fit so that the mass-spring-damper system behaves like the lowest harmonic of a vibrating string.

Figure 2: Mass-spring-damper system implementing a lightly-damped oscillator.

Apply Newton's second law $F=m\ddot{x}$, Hooke's law $F=Kx$, and the idealized friction law $F=R\dot{x}$, we obtain the dynamics of the forced oscillator as follows:

$$m\ddot{x} + R\dot{x} + Kx = F$$ (1)

In other words, the applied force $F$ is balanced at all times by the sum of the resisting inertial, friction, and spring forces. In the case when $F=0$, there are no external forces acting on the system. We have $f_0 \approx \sqrt{\frac{K}{m}}$ and the decay time constant $\tau = \frac{2m}{R}$.

However, if we implement the feedback law $F = P_D\dot{x} + P_Px$, then we arrive at the following differential equation [2]:

$$m\ddot{x} + (R-P_D)\dot{x} + (K-P_P)x = 0$$ (2)

This feedback can be realized physically by using a sensor to measure the displacement $x$, scaling $x$ by $P_P$, and adding the result to $\dot{x}$ scaled by $P_D$. The signal processing can be implemented using simple op-amp circuits, and the output signal can be fed to a motor that exerts the force $F$. This controlled system is equivalent to a system with friction coefficient $\hat{R}=R-P_D$ and spring constant $\hat{K}=K-P_P$. 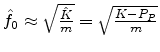As a result, we have $\hat{f_0} \approx \sqrt{\frac{\hat{K}}{m}} = \sqrt{\frac{K-P_P}{m}}$ and the decay time constant $\hat{\tau} = \frac{2m}{R-P_D}$.

If instead we use $F = P_D \int{x\,dt}$, then we have

$$\hat{\tau} \approx \frac{2m}{R+\frac{P_I}{4\pi^2f_0^2}}$$

although the analysis is more complicated [1]. Implementing $F = P_Px + P_I\int{x\,dt} + P_D\dot{x}$ is known as proportional-integral-derivative (PID) control. These controllers are often used to modify the system dynamics since the controller is simple and the user may freely choose the parameters $P_P,$ $P_I,$ and $P_D.$

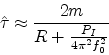
In summary, for a single lightly damped oscillator, $P_P$ may be used to alter the frequency of vibration $f_0,$ and $P_I$ and $P_D$ alter the damping. Note that integral control $P_I$ will do better at damping resonances with lower frequencies because integration provides a frequency weighting by $1/\omega$ (since $\int\cos(\omega t) = (1/\omega)\sin(\omega t)$, where $\omega=2\pi f$ is radian frequency).