Next |
Prev |
Up |
Top
|
REALSIMPLE Top
If we want an impulse at the sampling distance of where the pluck position of the guitar
would be, we calculate 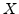 such that the samples for each delay line tapped into
correspond to the same physical location of the instrument [19]. We then set
such that the samples for each delay line tapped into
correspond to the same physical location of the instrument [19]. We then set 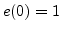 and
and 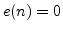 for all
for all 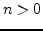 .
.
As Karplus-Strong discussed, exciting a digital waveguide with an impulse is psychoacoustically
plain, whereas exciting the digital waveguide with random values
results in a more satisfying sound [20].
With delay lines modeling displacement, we can
linearly-interpolate between the pluck-point to the two ends of the string for both
traveling waves for an excitation that displaces the string at a single point causing the
remainder of the string to displace linearly to the ends of the string.
Furthermore, if the delay lines represent acceleration or curvature, this
ideal-pluck is a single non-zero sample in each delay line. Note, since
the digital waveguide is a sampled model of a continuous system, band-limiting
conditions need be accounted for. A detailed
description of such can be found in
http://ccrma.stanford.edu/~jos/pasp/Ideal_Plucked_String.html.
Next |
Prev |
Up |
Top
|
REALSIMPLE Top
Download phys_mod_overview.pdf