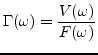Driving-Point Admittance

The driving-point admittance of the body of the instrument, characterizes linear-interactions between the string and the body in both directions: meaning energy transferred from both string to body and body to string. The driving-point admittance is defined as follows:

$$\Gamma(\omega) = \frac{V(\omega)}{F(\omega)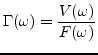}$$ (3)

where for a given frequency $\omega$ , the ratio between the Fourier Transform of the velocity and force is known. A physical explanation of the driving-point admittance is to view the admittance as a measure of how readily force exerted at the contact point at a certain frequency results in motion at that same frequency [23]. Since the body of the guitar is a rigid structure that exhibits standing waves at particular frequencies, known as the modes of the guitar, the body vibrates naturally at these frequencies. Notable modes include the air mode and the first few body modes.

A brief overview of the mechanics of our physical model thus far: the string vibrates upon excitation. Its end is connected to the body of the instrument at the bridge, exerting energy from the initial pluck at the fundamental frequency and its harmonic series. According to the driving-point admittance, the force applied at the bridge by the string results in motion of the bridge and top-plate. The resulting motion is dependent upon the construction of the top-plate of the instrument which determines its modes of vibration. The acoustic instrument then propagates pressure waves according to its top-plate movement, thereby coloring the resulting pressure waves heard by our ears.