The Digital CryBaby in Faust

The following Faust code approximately interpolates among the three measured pedal settings as a function of a single ``wah'' variable normalized to lie between 0 and 1:

 Q  = pow(2.0,(2.0*(1.0-wah)+1.0));
 fr = 450.0*pow(2.0,2.3*wah);
 g  = 0.1*pow(4.0,wah);

Closed-form expressions for biquad coefficients in terms of (Q,fr,g) based on 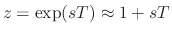$z = \exp(s T) \approx 1 + sT$ (low-frequency resonance assumed) yield the following Faust code:

 // BiQuad fit using z = exp(s T) ~ 1 + sT for low frequencies:
 frn = fr/SR; // Normalized pole frequency
 R = 1 - PI*frn/Q; // pole radius
 theta = 2*PI*frn; // pole angle
 a1 = -2.0*R*cos(theta); // biquad coeff
 a2 = R*R;               // biquad coeff
 // biquad denominator A = [1 a1 a2];

Finally, each time-varying biquad coefficient was smoothed by a unity-gain one-pole smoother with pole at 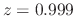$z=0.999$.

A Faust program implementing the digital approximation to the CryBaby wah pedal is shown Fig.21, and a test program is listed in Fig.22. The function crybaby(wah) is included in effect.lib starting with Faust version 0.9.9.3.

To test that the Faust version is producing the correct response, replace the last line in Fig.22 with the following:

  process = 1-1' : *(gs) : wahres;

The signal 1-1' is an impulse, so this process statement produces the impulse response of the wah model at its default setting (wah = 0.1) which can be edited to check different values. The amplitude response can then be seen by running

  faust2octave tcrybaby.dsp

followed by (in Octave)

  freqz(faustout);

Figure 21: Listing of Faust program tcrybaby.dsp for testing the Digital CryBaby wah pedal.

 

// Excerpt from effect.lib (Faust 0.9.9.3)
//
//------------------------ crybaby(wah) -----------------------------
// Digitized CryBaby wah pedal
// USAGE: crybaby(wah), where wah = "pedal angle" from 0 to 1.
// Requires filter.lib.
// Reference "http://ccrma.stanford.edu/~jos/pasp/vegf.html";
//
crybaby(wah) = *(gs(s)) : tf2(1,-1,0,a1s(s),a2s(s))
with {
  s = 0.999; // smoothing parameter (one-pole pole location)
  Q  = pow(2.0,(2.0*(1.0-wah)+1.0)); // Resonance "quality factor"
  fr = 450.0*pow(2.0,2.3*wah);       // Resonance tuning
  g  = 0.1*pow(4.0,wah);             // gain (optional)

  // BiQuad fit using z = exp(s T) ~ 1 + sT for low frequencies:
  frn = fr/SR; // Normalized pole frequency (cycles per sample)
  R = 1 - PI*frn/Q; // pole radius
  theta = 2*PI*frn; // pole angle
  a1 = 0-2.0*R*cos(theta); // biquad coeff
  a2 = R*R;                // biquad coeff

  // dezippering of slider-driven signals:
  a1s(s) = a1 : smooth(s);
  a2s(s) = a2 : smooth(s);
  gs(s) =  g  : smooth(s);
};

Figure 22: Listing of Faust program tcrybaby.dsp for testing the Digital CryBaby wah pedal.

 

// tcrybaby.dsp = test patch for digitized CryBaby pedal.

import("effect.lib"); // Faust 0.9.9.3 and higher

g    = hslider("level [midi: ctrl 0x7]",0.1,0,1,0.01);
wah  = hslider("wah [midi: ctrl 0x71]",0.4,0,1,0.01);
// MIDI Controller 0x71 is often "resonance" or "timbre"

// Some VST plugin hosts require stereo in and out:
process = + : *(g) : crybaby(wah) <: _,_;

// faust2octave impulse-response test using default wah-slider value:
// process = 1-1' : crybaby(wah);